Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


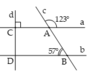
C A B ^ + A B D ^ = 180 0 ⇒ a // b
Mà d ⊥ a ⇒ d ⊥ b . Do đó d ⊥ a .

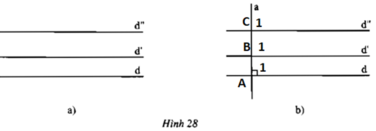
Vì a vuông góc với d ⇒ ∠A1 = 90o
• a có vuông góc với d’
Vì d//d’ ⇒ ∠A1 = ∠B1 ( hai góc đồng vị)
⇒ ∠B1 = 90o
• a có vuông góc với d’’
Vì d//d’’ ⇒ ∠A1 = ∠C1 (hai góc đồng vị)
⇒∠C1 = 90o
• d’ có song song với d’’
Vì ∠B1 = ∠C1 = 90o mà hai góc ở vị trí đồng vị

1) c vuông góc với b vì d//c và d vuông góc với b
(Ta nói được như trên vì ta có tính chất sau: khi hai đường thẳng song song với nhau và có một đường thẳng vuông góc với đường thẳng thứ ba thì đường thẳng còn lại cũng vuông góc với đường thẳng đó)
2) c có vuông góc với b vì b//a và c vuông góc với a
(Ta nói được như trên vì ta có tính chất sau: khi hai đường thẳng song song với nhau và có một đường thẳng vuông góc với đường thẳng thứ ba thì đường thẳng còn lại cũng vuông góc với đường thẳng đó)

b: c cắt a và b và tạo thành 1 cặp góc so le trong bằng nhau
nên a//b
mà d vuông góc a
nên d vuông góc b

A B C D E H O I K F M
a) Xét tam giác ADC và tam giác ABE
có AD=AB (GT)
góc DAC=góc EAB = ( 90 độ + góc BAC)
AE=AC ( GT)
tam giác ADC =tam giác ABE (C..G.C) (1)
suy ra DC = BE
góc ADC= góc ABC (2 góc tương ứng) (2)
DC cắt BE tại O
Xét tam giác ADF vuông tại A suy ra góc ADF + góc DFA = 90độ (3)
MÀ góc AFD = góc BFC ( đối đỉnh) (4)
Từ (2), (3), (4) suy ra góc BFC + góc ABE = 90 độ suy ra tam giác BFO vuông tại O suy ra DC vuông góc với BE tại O
b) Xét tam giác vuông IDA và tam giác vuông HAB
có AB=AD (GT)
góc IAD=góc ABH ( cùng phụ với góc HAB)
suy ra tam giác IDA = tam giác HAB (cạnh huyền-góc nhọn)
c) Chứng minh tương tự tam giác AEK = tam giác CAH (cạnh huyền-góc nhon)
suy ra EK = AH
Vì EK vuông góc với d
DI vuông góc với d
suy ra EK // DI
Xét tam giác vuông DIM và tam giác vuông EKM
có EK =DI (=AH)
góc IDM = góc IEK ( so le trong do EK // DI)
tam giác DIM = tam giác EKM (G.C.G)
suy ra DM=ME ; MI = MK
suy ra điều phải chứng minh

Trả lời
bạn tham khảo câu hỏi tương tự nha !
Có câu trả lời đó !
Đừng ném gạch chọi đá nha !
doc de nghe ki ki vay co sai de khong do chua cho dieu kien duong thang a hoi ai lam duoc gg