Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình vẽ bạn tự vẽ nha
Trước hết chứng minh :(tự chứng minh lun)
Cho tam giác ABC vuông cân tại A . Chứng minh \(\sqrt{2}\cdot AB=BC\)(*)
Xét tam giác KDM và tam giác IEM ta có:
KM=MI (gt)
KMD= IME (gt);
MD=ME (gt);
=> tam giác KDM = tam giác IEM (c.g.c);
=> KD= EI (tương ứng);
Lại có NMP=90 (gt) => NMK+ KMP=90
=> IME+ KMP =90 => IMK =90 mà KM=MI
=> tam giác KMI vuông cân tại M
Xét tam giác NMP vuông cân tại M có MNH=45 mà MHN=90 (do MH là đường cao)
=>Tam giác MHN vuông cân tại H
Áp dụng (*) vào tam giác KMI vuông cân tại M và tam giác MHN vuông cân tại H ta được:
\(\hept{\begin{cases}\sqrt{2}\cdot MH=MN\\\sqrt{2}\cdot KM=KI\end{cases}}\)mà \(KM\ge MH\)
\(\Rightarrow KI\ge MN\)
Xét 3 điểm K,E,I ta có:
\(KE+EI\ge KI\)
hay \(KE+KD\ge MN\)
Hoàng Nguyễn Văn Dòng thứ 5 dưới lên sai rồi mem,tự coi lại nha,không thể như thế được đâu.Tại sao \(KM\ge MH\) lại suy ra \(KI\ge MN\) được ??

.
.
.nônnonononononnnnonnnononnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnooooooooooooooooo
.
.
.

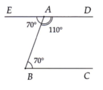
a: AD//BC
AE//BC
mà AD và AE có điểm chung là A
nên A,D,E thẳng hàng
b: Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)(định lí tổng ba góc trong một tam giác)
Tương tự 3