Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét ΔBAD va ΔBHD
Có BA=BH;BD là cạnh chung;gocABD=goc HBD→ΔBAD=ΔBHD(c-g-c)
→góc BAD=gocBHD(góc tương ứng)
→góc BAD=gocBAH=90 độ→DH vuông góc với BC
b)ΔBAD=ΔBHD(phần a)→gocADB=gocHDB
→ADB=HDB=110 chia 2=55 độ
Xét ΔABD .Có góc A + gocABD + goc BDA=180 do
→goc ABD=180-90-55=35 do

a) Xét ΔOAHΔOAH và ΔOBHΔOBH ta có:
OA = OB (theo giả thiết)
HA = HB (H là trung điểm AB)
OH chung
⇒ΔOAH=ΔOBH(c−c−c)⇒ΔOAH=ΔOBH(c−c−c)
b) Ta có: ΔOAH=ΔOBHΔOAH=ΔOBH (chứng minh trên)
⇒∠AOH=∠BOH⇒∠AOH=∠BOH ( 2 góc tương ứng bằng nhau)
Hay ∠AOC=∠BOC∠AOC=∠BOC
Xét ΔOACΔOAC và ΔOBCΔOBC ta có:
OA = OB (theo giả thiết)
OC chung
∠AOC=∠BOC∠AOC=∠BOC
⇒ΔOAC=ΔOBC(c−g−c)⇒ΔOAC=ΔOBC(c−g−c)
⇒∠OAC=∠OBC⇒∠OAC=∠OBC(2 góc tương ứng)
Mà ∠OAC∠OAC= 900 nên ∠OBC∠OBC = 900
⇒CB⊥OB⇒CB⊥OB( điều phải chứng minh)
c) Ta có: ∠AOC=∠BOC∠AOC=∠BOC (chứng minh trên) (1)
Xét 2 tam giác vuông MIO và MIH ta có:
MI chung
IO = IH (Vì I là trung điểm của OH)
⇒ΔMIO=ΔMIH⇒ΔMIO=ΔMIH (Cạnh góc vuông – cạnh góc vuông)
⇒∠MOI=∠MHI⇒∠MOI=∠MHI (2 góc tương ứng)
Hay∠AOC=∠MHIHay∠AOC=∠MHI (2)
Từ (1) và (2) ta có: ∠BOC=∠MHI∠BOC=∠MHI (cặp góc ở vị trí so le trong)
⇒MH//OB⇒MH//OB (*)
Lại có:
HK⊥BCOB⊥BC}⇒HK//OBHK⊥BCOB⊥BC}⇒HK//OB (Quan hệ giữa tính vuông góc và tính song song của ba đường thẳng) (**)
Từ (*) và (**) ta có: MH và HK cùng thuộc một đường thẳng song song với OB.
Suy ra M, H, K thẳng hàng (điều phải chứng minh)
x O y A B H C
a) Xét tam giác AHO và tam giác BHO
có OH chung
HA=HB (GT)
OA=OB (GT)
suy ra tam giác AHO = tam giác BHO (c.c.c) (1)
b) Từ (1) suy ra góc AOC = góc BOC
Xét tam giác AOC và tam giác BOC có
OC chung
góc AOC = góc BOC
OA=OB (GT)
suy ra tam giác AOC = tam giác BOC (c.g.c)
suy ra góc OAC = góc OBC (hai góc tương ứng)
mà góc OAC =900
suy ra góc OBC = 900
suy ra CB vuông góc với OB tại B

Ta có: \(\widehat{EMN}+\widehat{aMb}=180^o\) (kề bù)
\(\Rightarrow120^o+\widehat{aMb}=180^o\)
\(\Rightarrow\widehat{aMb}=180^o-120^o=60^o\)
Mà: \(\widehat{MNF}=60^o\)
Và: \(\widehat{aMb}\) và \(\widehat{MNF}\) so le trong
Vậy: a//b
Ta lại có: \(\begin{cases}b\perp c\\a\text{//}b\end{cases}\) \(\Rightarrow a\perp c\left(\text{đ}pcm\right)\)
Ta có:
góc M + góc N = 120o + 60o
= 180o
Mà góc M và góc N là 2 góc trong cùng phía
=> a // b
Mà \(b\perp c\) tại F => \(a\perp c\) (đpcm)

anh có phải là Ngô Dương Hoàng Châu đã từng học trường lộc trì phải không?
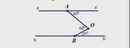





Kẻ tia \(Ox//aa'\) (\(Ox\)nằm giữa \(OA\)và \(OB\))
\(Ox//aa'\)suy ra \(\widehat{a'AO}=\widehat{AOx}\)(hai góc so le trong)
\(\widehat{BOx}=\widehat{AOB}-\widehat{AOx}=68^o-40^o=28^o\)
Suy ra \(\widehat{BOx}=\widehat{OBb'}\)
mà hai góc này ở vị trí so le trong nên \(Ox//bb'\).
Suy ra \(aa'//bb'\).
\(OH\perp aa'\)suy ra \(OH\perp bb'\)vì \(aa'//bb'\).