Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
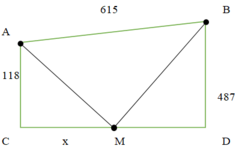
Cách 1: Giải bằng hàm số
Đặt CM = x (x > 0)
Dễ tính ra CD = 615 2 - ( 487 - 118 ) 2 = 492
Từ đề bài ta có: f(x) = x 2 + 118 2 + ( 492 - x ) 2 + 487 2
Quãng đường ngắn nhất người đó có thể đi
⇔ Giá trị nhỏ nhất của f(x) trên (0;492)
Ta có: f’(x) = - 2 x 2 x 2 + 118 2 + 2 ( 492 - x ) 2 ( 492 - x ) 2 + 487 2
⇒ f’(x) = 0
⇔ ( 492 - x ) x 2 + 118 2 - x ( 492 - x ) 2 + 487 2 = 0
⇔ ( 492 - x ) 2 ( x 2 + 118 2 ) - x 2 ( ( 492 - x ) 2 + 487 2 ) = 0
⇔ x = 58056 605
Ta có bảng biến thiên
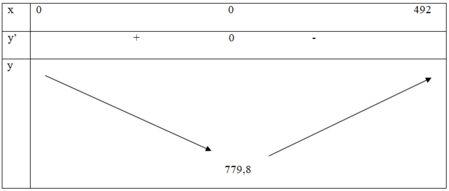
Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8
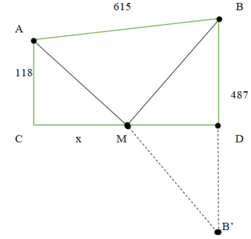
Cách 2: Giải bằng hình học
Gọi B’ là điểm đối xứng của B qua D
Dễ thấy AM + MB = AM + MB’
⇒ AM + MB ngắn nhất
⇒ AM + MB’ ngắn nhất
Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’
=>AM + MB’ ngắn nhất ó AM + MB’ = AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng

Đáp án A
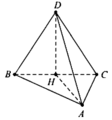
Gọi H là trung điểm của BC, O là tâm đường tròn ngoại tiếp tam giác ABC suy ra H là trung điểm của AO.
Ta có D H = 3. V A B C D S Δ A B C = a 3 4 .
Gọi J là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Khi đó J O ⊥ A B C .
Do J A = R , O A = a nên J O = R 2 − a 2 .
Mặt khác H O ⊥ J O , H O ⊥ H D nên ta có
a 3 4 ± R 2 − a 2 2 + a 2 2 = R 2 ⇔ R = a 91 8 .

Đáp án A.
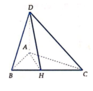
Từ dữ liệu đề bài ta thấy A B 2 + A C 2 = B C 2 ⇒ tam giác ABC vuông tại A.
Trong mặt phẳng A B C kẻ A H ⊥ B C tại H.
Ta có D A ⊥ B C A H ⊥ B C D A ∈ D A H ; A H ∈ D A H D A ∩ A H = A ⇒ D H ⊥ B C (định lý ba đường vuông góc).
Ta có A B C ∩ D B C = B C A H ⊥ B C ; D H ⊥ B C A H ∈ A B C ; D H ∈ D B C ⇒ A B C , D B C ^ = A H D ^ .
Ta có A H = A B . A C B C = 3 a .4 a 5 a = 12 a 5 .
Tam giác ADH vuông tại A.
⇒ tan A H D ^ = D A A H = 3. V A B C D S A B C 12 a 5 = 3.24 3 a 3 15. 1 2 .3 a .4 a 12 a 5 = 3 3
⇒ A H D ^ = 30 °
Vậy ta chọn A.

Đáp án B
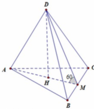
Gọi M là trung điểm của BC khi đó D M ⊥ B C A M ⊥ B C
Suy ra B C ⊥ ( D M A ) ⇒ D B C ; A B C ^ = 60 °
Lại có D M = A M = a 3 2
Dựng D H ⊥ A M ⇒ D H ⊥ ( A B C )
Khi đó V A B C D = 1 3 D H . S A B C = 1 3 D M . sin 60 ° . a 2 3 4 = a 2 3 16 .

Đáp án B
V A . B C D = 1 3 A D . S A B C = 1 6 A B . A C . A D = a b c 6



Đáp án A