Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

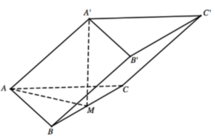
Gọi D là trung điểm AB \(\Rightarrow A'D\perp\left(ABC\right)\)
\(\Rightarrow CD\) là hình chiếu vuông góc của A'C lên (ABC)
\(\Rightarrow\widehat{A'CD}\) là góc giữa A'C và (ABC) \(\Rightarrow\widehat{A'CD}=60^0\)
\(CD=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
\(\Rightarrow A'D=CD.tan60^0=3a\)
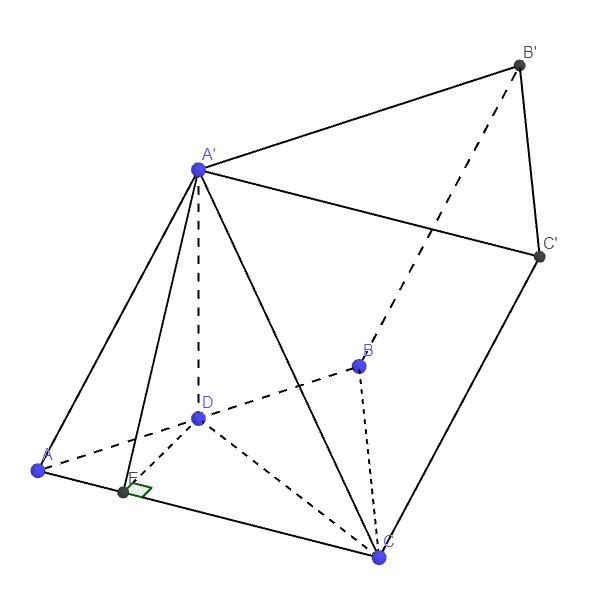
Từ D kẻ \(DE\perp AC\) (E thuộc AC)
Mà \(A'D\perp\left(ABC\right)\Rightarrow A'D\perp AC\)
\(\Rightarrow AC\perp\left(A'DE\right)\Rightarrow\widehat{AED}\) là góc giữa (A'AC) và (ABC)
\(DE=AD.sinA=a.sin60^0=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow A'E=\sqrt{A'D^2+DE^2}=\dfrac{a\sqrt{39}}{2}\)
\(\Rightarrow cos\widehat{A'ED}=\dfrac{DE}{A'E}=\dfrac{\sqrt{13}}{13}\)

a.
Do A' cách đều A,B,C \(\Rightarrow A'A=A'B=A'C\) hay \(A'ABC\) là chóp tam giác đều
\(\Rightarrow\) Hình chiếu vuông góc của A' lên (ABC) trùng trọng tâm ABC
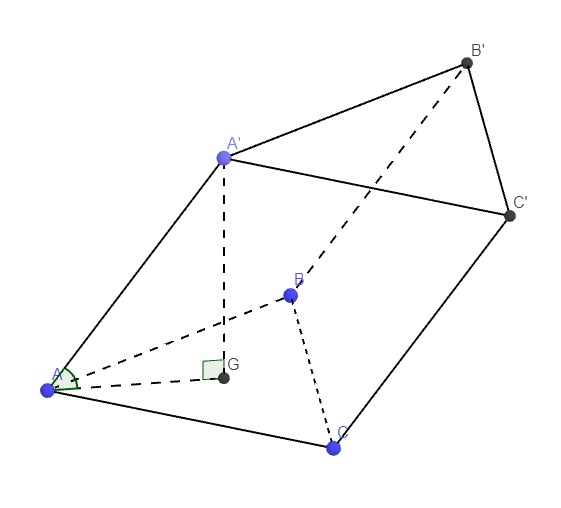
Gọi G là trọng tâm ABC \(\Rightarrow A'G\perp\left(ABC\right)\)
\(\Rightarrow A'G\) là đường cao lăng trụ
Lại có \(A'G\perp\left(ABC\right)\Rightarrow AG\) là hình chiếu vuông góc của A'A lên (ABC)
\(\Rightarrow\widehat{A'AG}\) là góc giữa A'A và (ABC) \(\Rightarrow\widehat{A'AG}=60^0\)
\(AG=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow A'G=AG.tan60^0=a\)
b.
Đề bài thật kì quặc, ở giả thiết đã cho sẵn góc giữa A'A và (ABC) là 60 độ sao còn bắt tính?
Còn góc đó chúng ta đã xác định ở câu a là \(\widehat{A'AG}\)

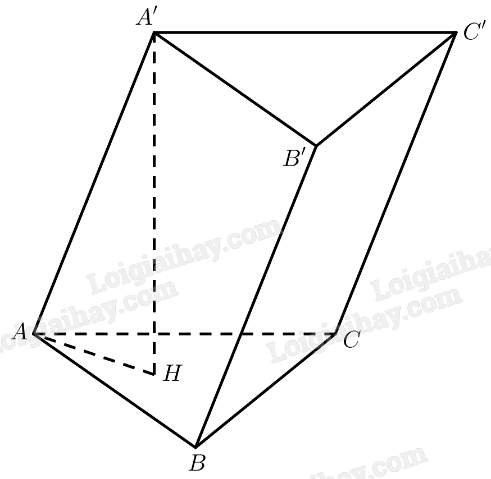
Gọi \(H\) là hình chiếu vuông góc của \(A'\) lên \(\left( {ABC} \right)\)
\(\begin{array}{l} \Rightarrow A'H \bot \left( {ABC} \right)\\ \Rightarrow \left( {AA',\left( {ABC} \right)} \right) = \left( {AA',AH} \right) = \widehat {A'AH}\end{array}\)
\(\Delta AA'H\) vuông tại \(H \Rightarrow A'H = AA'.\sin \widehat {A'AH} = \frac{{a\sqrt 3 }}{2}\)
Vì \(\left( {ABC} \right)\parallel \left( {A'B'C'} \right)\) nên \(d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = d\left( {A',\left( {ABC} \right)} \right) = A'H = \frac{{a\sqrt 3 }}{2}\)



AF=2a em ấn nhầm á. chứ k có ý đó đâu