Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(S_{ABCD}=12,5\times6,72=84\) ( cm2 )
Gọi độ dài hai đường chéo hình thoi là \(a\) và \(b\) ( a > b > 0 )
Khi đó :
\(\frac{1}{a}ab=84\)
\(\Leftrightarrow2ab=336\)
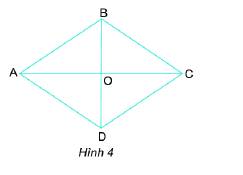
Gọi giao điểm 2 đường chéo là O .
Vì ABCD là hình thoi nên AC vuông góc BD
\(\Rightarrow\) Tam giác AOB vuông tại O
\(\Rightarrow\)\(AB^2=OA^2+OB^2\)
Mà \(OA=\frac{1}{2}b;OB=\frac{1}{2}a\)( Do tứ giác ABCDABCD là hình thoi )
Nên \(\frac{1}{4}\left(a^2+b^2\right)=12,5^2\)
\(\Leftrightarrow a^2+b^2=625\)
Ta có:
∙\(\hept{\begin{cases}a^2+b^2=625\Leftrightarrow a^2+b^2+2ab=625+336\Leftrightarrow\left(a+b\right)^2=961\Leftrightarrow a+b=31\\a^2+b^2=625\Leftrightarrow a^2+b^2-2ab=625-336\Leftrightarrow\left(a-b\right)^2=289\Leftrightarrow a-b=17\end{cases}}\)
Từ đó tính được \(a=24;b=7\)

Độ dài đường chéo BD là :
24 x 2/3 = 16 ( cm )
Diện tích hình thoi ABCD là :
24 x 16 : 2 = 192 ( cm2)
Đáp số : 192 cm2
Độ dài đường chéo BD là :
24 x \(\frac{2}{3}\) = 16 ( cm )
Diện tích hình thoi ABCD là :
24 x 16 : 2 = 192 ( cm2 )
Đáp số : 192 cm2

diện tích hình thoi là: (đổi 5m= 50 dm)
\(\dfrac{50\cdot20}{2}\) = 500(dm)
diện tích hình thoi ABCD là:
\(\dfrac{8\cdot6}{2}\) =24(cm)

Theo đề, ta có:\(5\cdot AC=6\cdot AD;5\cdot BD=8\cdot BC\) và AB=10cm
ABCD là hình thoi
=>AB=BC=CD=DA=10cm
\(AC=6\cdot AD=6\cdot10=60\left(cm\right)\)
\(5\cdot BD=8\cdot BC\)
=>\(BD=\dfrac{8}{5}\cdot BC=\dfrac{8}{5}\cdot10=16\left(cm\right)\)
Tổng độ dài hai đường chéo là:
60+16=76(cm)

a) Các cạnh của hình thoi bằng nhau.
b) Kẻ đường thẳng qua B và vuông góc với BC. Đặt êke có góc vuông tại điểm cắt nhau giữa đường thẳng vừa kẻ và AD, đặt một cạnh góc vuông của êke trùng với đường thẳng ta thấy cạnh góc vuông còn lại của êke trùng khít với cạnh AD.
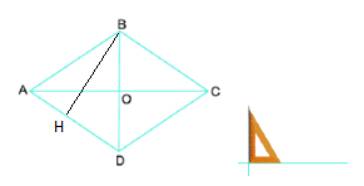
Khi đó BC và AD song song với nhau.
Tương tự AB và CD song song với nhau.
c) Tương tự như phần b, ta đặt đầu có góc vuông tại điểm O, đặt một cạnh góc vuông trùng với OB thì cạnh góc vuông còn lại trùng với OC hoặc OA. Khi đó AC và BD vuông góc với nhau.
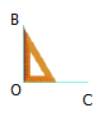

a) AB=CD; BC=AD.
b) Hai cặp cạnh AB và CD song song với nhau, BC và AD song song với nhau.
c) Sử dụng thước đo các cạnh ta thấy OA=OC; OB=OD.

a) Đáy lớn hình thang là:
8 + 6 = 14 cm
b) Chiều cao AH là:
( 6 + 8 ) : 2 = 7 cm
Diện tích hình thang ABCD là:
8 x 6 = 48 cm2
c) bạn tự làm nha!