Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử hình thang ABCD có đáy nhỏ AB = 15cm, cạnh bên AD = BC = 25cm

Mà ∆ ADH = ∆ BCK (cạnh huyền, cạnh góc vuông)
Suy ra: DH = CK = 12,5 (cm)
Chu vi hình thang ABCD là:
AB + BC + CD + DA = AB + BC + (CK + KH + HD) + DA
= 15 + 25 + (12,5 + 15 + 12,5) + 25 = 105 (cm)
Chu vi hình thang ABCD là:
![]()

gọi hình thang đó là ABCD (AB//CD),AB=15, AD=BC=25
góc DAB=góc ABC=120 độ.
kẻ AH, BK vuông góc với CD (H,K thộc CD)
=>HK=AB=15 (cm)
xét tam giác AHD có: AD=25, góc D=60 độ
=>DH=AD.cos=AD/2=12.5 (cm)
tương tự ta có CK=12.5 (cm)
=>CD=CK+DH+HK=12.5+12.5+15=40 (cm)
=>chu vi ABCD=AB+BC+CD+DA=105 (cm)
gọi hình thang đó là ABCD (AB//CD),AB=15, AD=BC=25
góc DAB=góc ABC=120 độ.
kẻ AH, BK vuông góc với CD (H,K thộc CD)
=>HK=AB=15 (cm)
xét tam giác AHD có: AD=25, góc D=60 độ
=>DH=AD.cos=AD/2=12.5 (cm)
tương tự ta có CK=12.5 (cm)
=>CD=CK+DH+HK=12.5+12.5+15=40 (cm)
=>chu vi ABCD=AB+BC+CD+DA=105 (cm)

gọi hình thang đó là ABCD ( AB//CD và AB là đáy nhỏ)
theo đề bài thì hình thang này là hình thang cân
từ A;B kẻ AH;BK vuông góc vs BC ==>HK=15 cm
xét tam giác AHD có DH=1/2 AD =25/2=12,5 cm
do đó KC =DH=12,5 cm
==> CD=12,5+12,5+15=40 cm
áp dụng định lí py-ta go vao tam giác ADH tính được AH= \(\frac{25\sqrt{3}}{2}\) cm
do dó S hình thang là \(\frac{\left(40+15\right)\cdot\frac{25\sqrt{3}}{2}}{2}=\frac{55\cdot25\sqrt{3}}{4}\) cm2

Câu 11.12.
Kẻ đường cao \(AH,BK\).
Do tam giác \(\Delta AHD=\Delta BKC\left(ch-gn\right)\)nên \(DH=BK\).
Đặt \(AB=AH=x\left(cm\right),x>0\).
Suy ra \(DH=\frac{10-x}{2}\left(cm\right)\)
Xét tam giác \(AHD\)vuông tại \(H\):
\(AD^2=AH^2+HD^2=x^2+\left(\frac{10-x}{2}\right)^2\)(định lí Pythagore)
Xét tam giác \(DAC\)vuông tại \(A\)đường cao \(AH\):
\(AD^2=DH.DC=10.\left(\frac{10-x}{2}\right)\)
Suy ra \(x^2+\left(\frac{10-x}{2}\right)^2=10.\frac{10-x}{2}\)
\(\Leftrightarrow x=2\sqrt{5}\)(vì \(x>0\))
Vậy đường cao của hình thang là \(2\sqrt{5}cm\).
Câu 11.11.
Kẻ \(AE\perp AC,E\in CD\).
Khi đó \(AE//BD,AB//DE\)nên \(ABDE\)là hình bình hành.
Suy ra \(AE=BD=15\left(cm\right)\).
Kẻ đường cao \(AH\perp CD\)suy ra \(AH=12\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AH\):
\(\frac{1}{AH^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AE^2}=\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AC=20\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.15.20=150\left(cm^2\right)\),
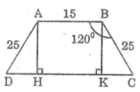
gọi hình thang đó là ABCD (AB//CD),AB=15, AD=BC=25
góc DAB=góc ABC=120 độ.
kẻ AH, BK vuông góc với CD (H,K thộc CD)
=>HK=AB=15 (cm)
xét tam giác AHD có: AD=25, góc D=60 độ
=>DH=AD.cos=AD/2=12.5 (cm)
tương tự ta có CK=12.5 (cm)
=>CD=CK+DH+HK=12.5+12.5+15=40 (cm)
=>chu vi ABCD=AB+BC+CD+DA=105 (cm)