K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

21 tháng 6 2016
Gọi I là trung điểm của DH. Dễ thấy tứ giác ABMI là hình bình hành, suy ra I là trực tâm của tam giác ADM. Từ đó suy ra BM vuông góc với DM
Phương trình BM:
\(\widehat{DM}=\left(\frac{22}{5}-2;\frac{14}{5}-2\right)=\left(\frac{12}{5};\frac{4}{5}\right)\)//(3;1)
(BM):\(3\left(x+\frac{22}{5}\right)+1\left(y-\frac{14}{5}\right)=0\)⇔(BM):3x+y−16=0
Tọa độ B là nghiệm hệ
\(\begin{cases}3-2y+4=0\\3x+y-16=0\end{cases}\)<=> \(\begin{cases}x=4\\y=4\end{cases}\)=>B(4;4)
Gọi K là giao điểm của BD và AC. Ta có \(\overrightarrow{KB}=-\frac{1}{2}\overrightarrow{KD}\)
Tọa độ K
\(\begin{cases}x_K=\frac{4+\frac{1}{2}.2}{1+\frac{1}{2}}=\frac{10}{3}\\y_K=\frac{4+\frac{1}{2}.2}{1+\frac{1}{2}}=\frac{10}{3}\end{cases}\)=> K(\(\frac{10}{3};\frac{10}{3}\))
Phương trình AC:
\(\overrightarrow{KM}=\left(\frac{16}{15};-\frac{8}{15}\right)\)//(2;−1)
(AC):x+2y−10=0
Phương trình DI:
(DI):2(x−2)−(y−2)=0⇔(DI):2x−y−2=0
Tọa độ H là nghiệm hệ
\(\begin{cases}x+2y-10=0\\2x-y-2=0\end{cases}\)<=>\(\begin{cases}x=\frac{14}{5}\\y=\frac{18}{5}\end{cases}\)
Tọa độ điểm C→C(6;2)
Ta có
\(\overrightarrow{BA}=\frac{1}{2}\overrightarrow{CD}\),<=>\(\begin{cases}x_A=\frac{1}{2}\left(2-6\right)+4=2\\y_A=\frac{1}{2}\left(2-2\right)+4=4\end{cases}\)→A(2;4)

CM
19 tháng 2 2017
Chọn C.
Do I là trung điểm của DC nên ta có:
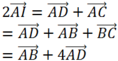
Lại có:
![]()
suy ra
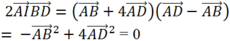
Vậy AI ⊥ BD.
a) Để \(AC\perp BD\) thì \(\Rightarrow\overrightarrow{AC}\cdot\overrightarrow{BD}=0\Rightarrow\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}\right)=0\\ \Rightarrow\overrightarrow{AB}\cdot\overrightarrow{BA}+\overrightarrow{BC}\cdot\overrightarrow{BA}+\overrightarrow{AB}\cdot\overrightarrow{AD}+\overrightarrow{BC}\cdot\overrightarrow{AD}=0\\ \Rightarrow-h^2+0+0+ab=0\\ \Rightarrow h^2=ab\)
b) Để \(AI\perp BI\) thì \(\Rightarrow\overrightarrow{AI}\cdot\overrightarrow{BI}=0\Rightarrow\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{AC}\right)\dfrac{1}{2}\left(\overrightarrow{BD}+\overrightarrow{BC}\right)=0\\ \Rightarrow\left(\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{BC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{BC}\right)=0\\ \\ \Rightarrow\overrightarrow{AD}\cdot\overrightarrow{BA}+\overrightarrow{AB}\cdot\overrightarrow{BA}+\overrightarrow{BC}\cdot\overrightarrow{BA}+\overrightarrow{AD}\cdot\overrightarrow{AD}+\overrightarrow{AB}\cdot\overrightarrow{AD}+\overrightarrow{BC}\cdot\overrightarrow{AD}+\overrightarrow{AD}\cdot\overrightarrow{BC}+\overrightarrow{AB}\cdot\overrightarrow{BC}+\overrightarrow{BC}\cdot\overrightarrow{BC}=0\\ \Rightarrow-h^2+a^2+ab+ab+b^2=0\\ \Rightarrow a^2+2ab+b^2=\left(a+b\right)^2=h^2\\ \Rightarrow a+b=h\)
siêng quá nhở :)))))