Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
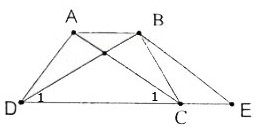
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra  =
=  (3)
(3)
∆BDE cân tại B (câu a) nên  =
=  (4)
(4)
Từ (3) và (4) suy ra  =
= 
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
=  (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 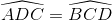
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Bài giải:
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:

AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra  =
=  (3)
(3)
∆BDE cân tại B (câu a) nên  =
=  (4)
(4)
Từ (3) và (4) suy ra  =
= 
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
=  (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 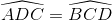
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

A B C D O 1 2 1 2 1 2
1. Xét tam giác ABD và tam giác ABC có:
AB chung
AD=BC ( ABCD là hình thang cân)
\(\widehat{A}=\widehat{B}\)( hai góc đối đỉnh)
=> Tam giác ABD= Tam giác ABC
2.
Ta có: Tam giác ABD= Tam giác ABC ( theo câu 1)
=> \(\widehat{A_1}=\widehat{B_2}\)
=> Tam giác OAB cân
=> OA=OB
3.
Ta có \(\widehat{D}=\widehat{C}\)( ABCD là hình thang cân)
=> \(\widehat{D_1}+\widehat{D_2}=\widehat{C_1}+\widehat{C_2}\)
Mà \(\widehat{D_1}=\widehat{C_1}\)( Tam giác ABD= Tam giác ABC)
=> \(\widehat{D_2}=\widehat{C_2}\)
=> Tam giác DOC cân tại O
=> DO=CO
Bài toán 8 mà sao giống toán 7 thế nhỉ?
A B C D O
a) Trong hình thang câng hai cạnh bên bằng nhau (AD = BC)
Hai góc kề ở 1 đáy bằng nhau nên theo tính chất hai đoạn thẳng song song suy ra hai góc kề ở đáy kia cũng bằng nhau.
Suy ra \(\widehat{A}=\widehat{B};\widehat{C}=\widehat{D}\)
Xét tam giác ABD và tam giác BAC có:
AD = BC (gt)
\(\widehat{A}=\widehat{B}\)
\(AB:\text{ cạnh chung }\)
\(\Rightarrow\Delta ABD=\Delta BAC\)
b) Do \(\Delta ABD=\Delta BAC\Rightarrow\widehat{DBA}=\widehat{BAC}\left(\text{hai góc tương ứng}\right)\)
\(\Rightarrow\Delta OAB\text{ cân tại O }\Rightarrow OA=OB\) (theo tính chất tam giác cân)
c) Cũng do \(\Delta ABD=\Delta BAC\Rightarrow BD=AC\Leftrightarrow OB+OD=OA+OC\)
Theo kết quả câu b ta có OA = OB suy ra OD = OC (đpcm)
Xét △ABD và △BAC có :
AD = BC (gt)
AB chung
^A = ^B (gt)
\(\Rightarrow\)△ABD = △BAC (cgc)
\(\Rightarrow\)^ADB = ^ BCA
Mà ^ADC = ^BCD
\(\Rightarrow\)^ODC = ^OCD
Lại có : AC ⊥ BD
\(\Rightarrow\)△OCD vuông cân tại O
Chứng minh tương tự với △OAB :
\(\Rightarrow\)ĐPCM
Áp dụng định lí Pitago vào △OAB vuông tại O có :
Có: OA2 + OB2 = AB2
=> 2OA2 = 16
=> OA = \(2\sqrt{2}\)cm
Tương tự: OD = \(4\sqrt{2}\)cm
Kẻ MN đi qua O và vuông góc với AB(tại M) và CD(tại N)
=> M là trung điểm AB ; N là trung điểm CD (vì ABCD là hình thang cân)
Có: OM2 = OA2 - AM2 = \(\left(2\sqrt{2}\right)^2-2^2\) = 8 - 4 = 4 cm
=> OM = 2cm
Tương tự chứng minh :
=> ON = 4 cm
=> MN = 6 cm
Vậy SABCD = \(\frac{\left(4+8\right).6}{2}=36\) cm2