Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là giao điểm của AC và BD.
Chứng minh: OE ^ AB.
Tương tự, có OF ^ CD.
Suy ra OF ^ AB. Vậy EF ^ AB
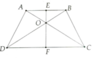


Do ABCD là hình thang cân
\(\Rightarrow AD=BC\) và \(\widehat{FDA}=\widehat{FCB}\)
Do F là trung điểm của CD (gt)
\(\Rightarrow FC=FD\)
Xét \(\Delta ADF\) và \(\Delta BCF\) có:
\(AD=BC\) (cmt)
\(\widehat{FDA}=\widehat{FCB}\) (cmt)
\(FD=FC\) (cmt)
\(\Rightarrow\Delta ADF=\Delta BCF\) (c-g-c)
\(\Rightarrow AF=BF\) (hai cạnh tương ứng)
\(\Delta FAB\) có:
\(AF=BF\) (cmt)
\(\Rightarrow\Delta FAB\) cân tại F
Lại có E là trung điểm của AB
\(\Rightarrow FE\) là đường trung tuyến của \(\Delta FAB\)
\(\Rightarrow FE\) cũng là đường cao của \(\Delta FAB\)
\(\Rightarrow FE\perp AB\)
Mà AB // CD (gt)
\(\Rightarrow FE\perp CD\)
Vậy EF vuông góc với AB và CD

Câu hỏi của headsot96 - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo!

a) Xét tam giác ACD có: AF=FC (gt) ; DK=KC (gt)
=> FK là đường trung bình của tam giác ACD
=> FK//AD
=> ADKF là hình thang
Chứng minh tương tự t cũng có: ME là đường trung bình của tam giác ABD
=> ME // AD mà FK//AD (cmt)
=> ME//FK (1)
Chứng minh tương tự ta cũng có:
MF là đường trung bình tam giác ABC , EK là đường trung bình tam giác DBC
=> MF//BC ; EK // BC
=> MF//EK (2)
Từ (1) và (2) ta có: EMFK là hình bình hành

- Hình vẽ:
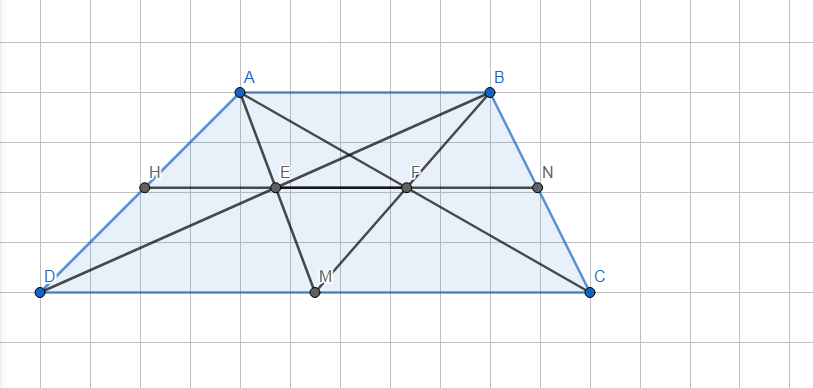
a) - Xét △EDM có:
AB//DM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) (định lí Ta-let) (1).
- Xét △FCM có:
AB//CM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{BF}{MF}=\dfrac{AB}{CM}\) (định lí Ta-let) (2).
- Từ (1) và (2) và \(CM=DM\) (M là trung điểm BC) suy ra:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\).
- Xét △ABM có:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\) (cmt)
=>\(EF\)//\(AB\) (định lí Ta-let đảo)nên\(EF\)//\(AB\)//\(CD\)
b) -Xét △ADM có:
HE//DM (cmt).
=>\(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (định lí Ta-let). (3)
- Xét △ACM có:
EF//CM (cmt)
=>\(\dfrac{EF}{CM}=\dfrac{AE}{AM}\) (định lí Ta-let) (4)
- Từ (3) và (4) và \(DM=CM\) (M là trung điểm BC) suy ra: \(HE=EF\)
-Xét △BDM có:
EF//DM (cmt).
=>\(\dfrac{EF}{DM}=\dfrac{BF}{BM}\)(định lí Ta-let). (5)
- Xét △BCM có:
NF//CM (cmt)
=>\(\dfrac{NF}{CM}=\dfrac{BF}{BM}\) (định lí Ta-let) (6)
- Từ (5) và (6) và \(CM=DM\) (M là trung điểm BC) suy ra: \(NF=EF\)
Mà \(HE=EF\) nên \(HE=EF=NF=\dfrac{1}{3}HN\).
c) -Ta có: \(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (cmt)
=>\(\dfrac{DM}{HE}=\dfrac{AM}{AE}\).
=>\(\dfrac{DM}{HE}-1=\dfrac{EM}{AE}\) (7)
- Ta có: \(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) nên \(\dfrac{EM}{AE}=\dfrac{DM}{AB}\). (8)
- Từ (7) và (8) suy ra:
\(\dfrac{DM}{HE}-1=\dfrac{DM}{AB}\)
=>\(\dfrac{DM}{HE}=\dfrac{DM}{AB}+1=\dfrac{DM+AB}{AB}\)
=>\(HE=\dfrac{AB.DM}{AB+DM}=\dfrac{7,5.\left(12.\dfrac{1}{2}\right)}{7,5+\left(12.\dfrac{1}{2}\right)}=\dfrac{10}{3}\)
=>\(HN=3HE=3.\dfrac{10}{3}=10\) (cm).

A B C D E F P
*Chứng minh EF // AB // CD
Gọi P là trung điểm AD có ngay:PF // AB (2) (PF là đường trung bình tam giác DAB)
Lại có PE // DC(là đường trung bình tam giác ADC) và DC // AB nên PE // AB(2)
Từ (1) và (2) theo tiên đề Ơclit suy ra P, E, F thẳng hàng. Mà PF // AB -> FE // AB(3)
Lại có PE // DC -> FE // DC (4). Từ (3) và (4) suy ra đpcm.
* Chứng minh EF = \(\frac{CD-AB}{2}=\frac{CD}{2}-\frac{AB}{2}\).
Do PE = 1/2 CD; PF = 1/2 AB và P, E, F thẳng hàng nên:
\(PF+FE=PE\Leftrightarrow\frac{1}{2}AB+FE=\frac{1}{2}CD\Leftrightarrow FE=\frac{CD-AB}{2}\)
=> đpcm
P/s: ko chắc.

Xét ΔADF và ΔBCF có
AD=BC
\(\widehat{D}=\widehat{C}\)
FD=FC
Do đó: ΔADF=ΔBCF
Suy ra: FA=FB
Xét ΔFAB có FA=FB
nên ΔFAB cân tại F
mà FE là đường trung tuyến ứng với cạnh đáy AB
nên FE là đường cao ứng với cạnh AB
hay FE\(\perp\)AB