Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tớ biết làm nè
.
.
.
.
.
.
.
.
.
.
.
Biết làm cl í, tin người vcl:))

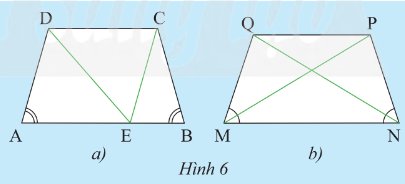
a) i) \(ABCD\) là hình thang cân (gt)
\( \Rightarrow \widehat A = \widehat B\) (1) và \(DC\) // \(AE\)
Vì \(AD\;{\rm{//}}\;CE\) (gt)
\(\widehat A = \widehat {CEB}\) (cặp góc đồng vị) (2)
Từ (1) và (2) suy ra: \(\widehat {CEB} = \widehat B\)
Suy ra \(\Delta CEB\) là tam giác cân.
ii) \(\Delta CEB\) cân tại \(C\) (cmt)
Suy ra: \(CE = BC\) (3)
Xét \(\Delta ADE\) và \(\Delta CED\) ta có:
\(\widehat {{\rm{ADE}}} = \widehat {{\rm{CED}}}\) (\(AD\)// \(CE\), cặp góc so le trong)
\(DE\) chung
\(\widehat {{\rm{AED}}} = \widehat {{\rm{CDE}}}\) (\(CD\) // \(AB\), cặp góc so le trong)
Suy ra: \(\Delta ADE = \Delta CED\) (g-c-g)
Suy ra: \(AD = CE\) (4)
Từ (3) và (4) suy ra: \(AD = BC\)
b) Chứng minh tương tự như ý a) ta có: Hình thang cân \(MNPQ\) có hai cạnh bên \(MQ = NP\)
Xét tam giác \(\Delta MQP\) và \(\Delta NPQ\) ta có:
\(MQ = NP\) (cmt)
\(\widehat {{\rm{MQP}}} = \widehat {{\rm{NPQ}}}\) (do \(MNPQ\) là hình thang cân)
\(PQ\) chung
Suy ra: \(\Delta MQP = \Delta NPQ\) (c-g-c)
\( \Rightarrow MP = NQ\) (hai cạnh tương ứng)

a: Xét tứ giác ABCH có
AB//CH
góc AHC=90 độ
Do đó: ABCH là hình thang vuông
b: Sửa đề; DH=CK
Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
góc D=góc C
Do đo: ΔAHD=ΔBKC
=>DH=CK
c: Xét ΔAED có
AH vừa là đường cao, vừa là trung tuyến
nên ΔAED cân tại A
=>góc AED=góc ADE=góc BCD
=>AE//BC
mà AB//CE
nên ABCE là hình bình hành

Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC
Ta thấy A gồm có 99 số hạng nên ta nhóm mỗi nhóm 3 số hạng.
Ta có: A = 1 + 5 + 52 + 53 + 54 + 55 +...+ 597 + 598 + 599
= (1 + 5 + 52 )+ (53 + 54 + 55 )+...+( 597 + 598 + 599 )
=(1 + 5 + 52 )+ 53(1 + 5 + 52 ) +...+ 597(1 + 5 + 52 )
= ( 1 + 5 + 52)(1 + 53+....+597)
= 31(1 + 53+....+597)
Vì có một thừa số là 31 nên A chia hết cho 31.
P/s Đừng để ý câu trả lời của mình