Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tam giác ABF có AE là phân giác đồng thời là đường cao nên nó là tam giác cân tại B.
Vây thì BA = BF.
b) Xét tứ giác HDKF có HF song song và bằng DK nên HDKF là hình bình hành.
Vậy nên HD // FK ; HD = FK
Xét tam giác ABC có AB < AC nên \(\widehat{ABC}>\widehat{ACB}\)

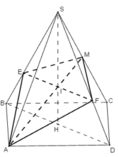
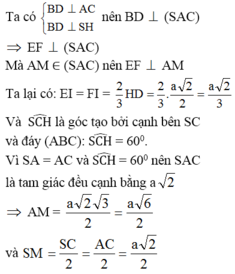

Điều này chứng tỏ SM là đường cao của hình chóp S.AEMF. Vậy thể tích của khối chóp S.AEMF là:
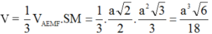

Để tính thể tích SAPMQ, ta cần tìm độ dài đoạn PM và đoạn MQ. Gọi E là trung điểm của BD. Ta có ME song song với AM và ME = 1/2 BD = 1/2 a. Vì (∆) song song với BD nên góc AME = góc ABD = 45 độ. Vì SA vuông góc với ABCD nên góc SAM = 90 độ. Vì SA = a√3 và góc SAM = 90 độ nên tam giác SAM là tam giác vuông cân tại A. Do đó, góc ASM = 45 độ. Vì góc ASM = góc AME = 45 độ nên tam giác ASM và tam giác AME đồng dạng. Vậy, ta có: AM/AS = AE/AM AM^2 = AS * AE AM^2 = (a√3) * (1/2 a) AM^2 = a^2 * √3 / 2 AM = a√3 / √2 AM = a√6 / 2 Ta có ME = 1/2 a Vậy, PM = AM - ME = (a√6 / 2) - (1/2 a) = (a√6 - a) / 2 Tương tự, ta có MQ = AM + ME = (a√6 / 2) + (1/2 a) = (a√6 + a) / 2 Vậy, thể tích SAPMQ = SABC * PM = a^2 * (a√6 - a) / 2 = a^3√6 / 2 - a^3 / 2

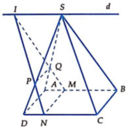
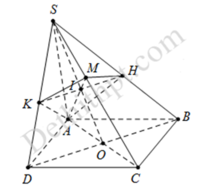
ình chóp S.ABCD là hình chóp đều nên chân H của đường cao SH chính là tâm của đáy. Mặt phẳng đi qua AM và song song với BD cắt mặt phẳng (SDB) theo một giao song song với BD, hay EF // BD.
Ta dựng giao tuyến EF như sau : Gọi I là giao điểm của AM và SH Qua I ta dựng một đường thẳng song song với BD, đường này cắt SB ở E và cắt SD ở F. Ta có góc SAH= 60°. Tam giác cân SAC có SA = SC và SAC = 60° nên nó là tam giác đều: I là giao điểm của các trung tuyến AM và SH nên: