Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D ? ?
Ta có: \(AB//CD\left(gt\right)\)
\(\Rightarrow\hept{\begin{cases}A+D=180^0\left(tcp\right)\\C+B=180^0\left(tcp\right)\end{cases}}\)mà \(\hept{\begin{cases}D=40^0\\B=80^0\end{cases}\left(gt\right)}\)
\(\Rightarrow\hept{\begin{cases}A=140^0\\C=100^0\end{cases}}\)
chúc bạn học tốt

Câu đầu thiếu dữ kiện em nhé!
----------
Do hình thang ABCD cân với AB và CD là hai đáy
⇒ ∠B = ∠A = 70⁰
∠D = ∠C = 100⁰
⇒ ∠A + ∠B + ∠C + ∠D = 340⁰
Vậy đề câu này cũng sai!

Do AB//CD
=) \(\widehat{A}\)+\(\widehat{D}\)=1800 (2 góc vị trí trong cùng phía )
1000 + \(\widehat{D}\)=1800
\(\widehat{D}\)=1800 - 1000
\(\widehat{D}\)= 800
Xét tứ giác ABCD có :
\(\widehat{A}\)+\(\widehat{B}\)+\(\widehat{C}\)+\(\widehat{D}\)=3600
1000+1200+\(\widehat{C}\)+800 =3600
3000 +\(\widehat{C}\)=3600
\(\widehat{C}\)= 600
2) Từ B kẻ BE \(\perp\)CD
Xét tam giác ADH (\(\widehat{AH\text{D}}\)=900) và BCE (\(\widehat{BEC}\)=900) có:
AD=BC (tính chất hình thang cân)
\(\widehat{A\text{D}H}\)=\(\widehat{BCE}\)(tính chất hình thang cân)
=) Tam giác ADH = Tam giác BCE (cạch huyền - góc nhọn )
=) DH= CE (2 cạch tương ứng )
Do AB//CD Mà AH\(\perp\)CD=) AH\(\perp\)AB
Xét tứ giác ABEH có
\(\widehat{BAH}\)= \(\widehat{AHE}\) = \(\widehat{BEH}\) = 900
=) Tứ giác ABEH lá hình chữ nhật =) AB=HE=10 cm
Ta có : DH+HE+EC= 20 cm
2DH+10=20
2DH =10
DH = 5 (cm)
xét tam giác vuông AHD
Áp dụng định lí Pitago ta có
AD2=AH2+HD2
AD2=122+52
AD2= 144+25=169
AD=13 cm (đpcm)


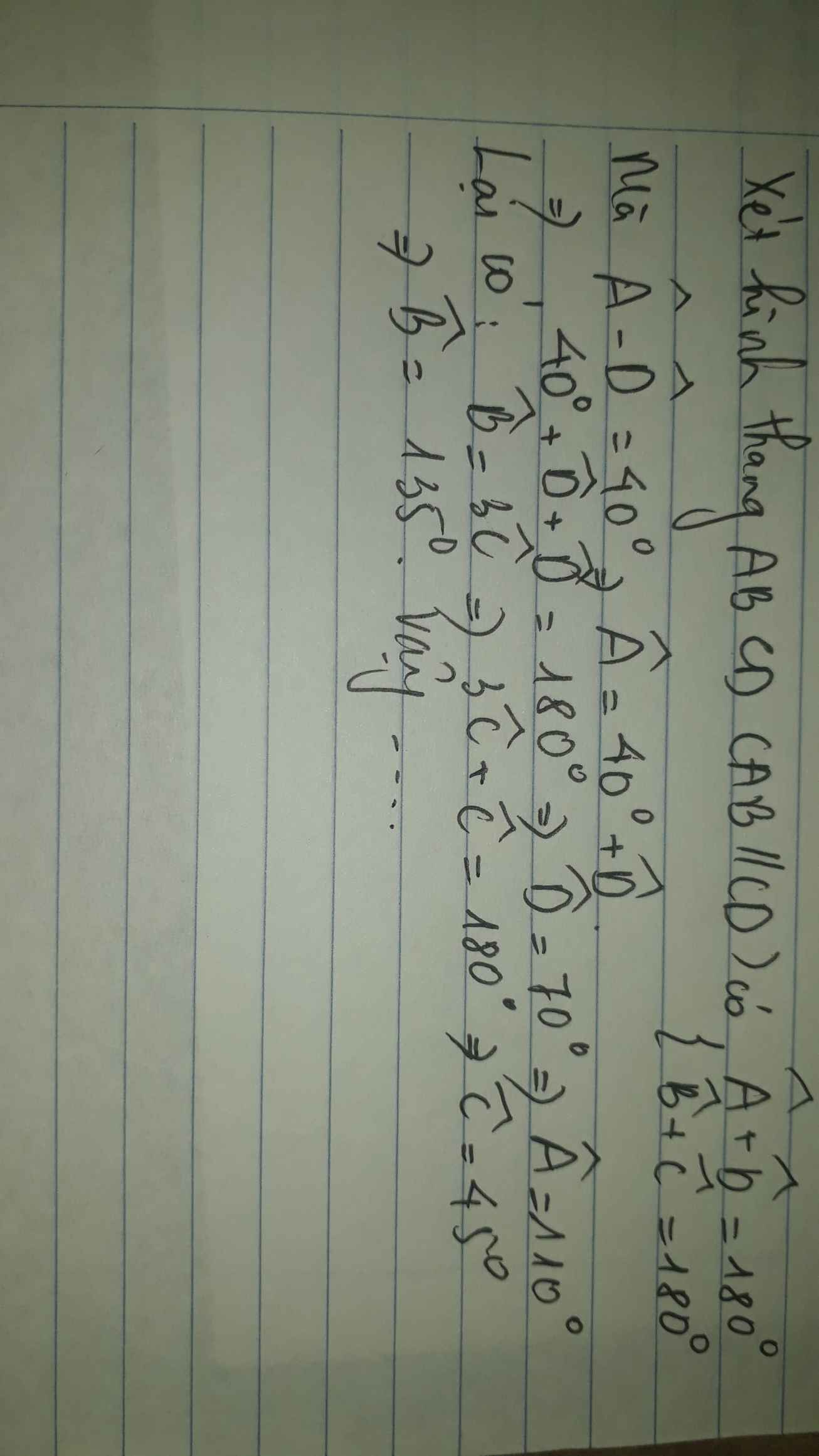
hihi
tính góc à