Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
Sửa đề; EA=6cm
Xét ΔEMD và ΔEBA có
góc EMD=góc EBA
góc MED=góc BEA
=>ΔEMD đồng dạng vơi ΔEBA
=>MD/BA=ED/EA
=>10/BA=8/6=4/3
=>BA=7,5cm
b: Xét ΔFMC và ΔFBA có
góc FMC=góc FBA
góc MFC=góc BFA
=>ΔFMC đồng dạng với ΔFBA
=>FM/FB=MC/BA=MD/BA=EM/EA
=>FE//AB

a) Chứng minh rằng AK= AC , BI=ID
Vì FE là đường trung bình thang nên FE//AB//CD
E,F là trung điểm của AB và BC nên AK= AC, BI=ID
( trong tam giác đường thẳng qua trung điểm của 1 cạnh,// với cạnh thứ 2 thì qua trung điểm cạnh thứ 3)
b) Cho AB = 6cm , CD = 10cm. Tính độ dài EI, KF, IK
EI = KF = 1/2.AB = 1/2.6 = 3 ( đường trung bình tam giác )
FE= (AB + CD)/2 = ( 10+6)/2 = 8
IK= FE - EI - KF = 8-3-3 = 2

A B C D E F I K
a ) Vì \(\hept{\begin{cases}EA=ED\left(gt\right)\\FB=FC\left(gt\right)\end{cases}}\)
\(\Rightarrow\) EF là đường trung bình của hình thang ABCD.
\(\Rightarrow\) EF // AB // CD
Xét \(\Delta ABC\) có : \(\hept{\begin{cases}BF=FC\\FK//AB\end{cases}}\)
\(\Rightarrow AK=KC\)
Xét \(\Delta ABD\) có : \(\hept{\begin{cases}AE=ED\\EI//AB\end{cases}}\)
\(\Rightarrow BI=ID\)
Vậy \(\hept{\begin{cases}AK=KC\\BI=ID\end{cases}\left(đpcm\right)}\)
b ) Vì EF là đường trung bình của hình thang ABCD.
\(\Rightarrow EF=\frac{CD+AB}{2}=\frac{10+6}{8}=2\left(cm\right)\)
Mặt khác, ta có :
* EI là đường trung bình của \(\Delta ABD\)
\(\Rightarrow EI=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)
* KF là đường trung bình của \(\Delta ABC\)
\(\Rightarrow KF=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)
Mà : EF = EI + IK + KF
\(\Rightarrow\) IK = EF - ( EI + KF ) = 8 - ( 3 + 3 ) = 2cm.
Vậy \(\hept{\begin{cases}EI=3cm\\KF=3cm\\IK=2cm\end{cases}}\)
Chúc bạn học tốt !!!

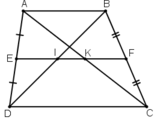
a) + Hình thang ABCD có EA = ED, FB = FC (gt)
⇒ EF là đường trung bình của hình thang ABCD.
⇒ EF // AB // CD
+ ΔABC có BF = FC (gt) và FK // AB (cmt)
⇒ AK = KC
+ ΔABD có: AE = ED (gt) và EI // AB (cmt)
⇒ BI = ID
b) + Vì EF là đường trung bình của hình thang ABCD.
⇒ EF = (AB + CD)/2 = (6 + 10)/2 = 8cm.
+ ΔABD có AE = ED, DI = IB
⇒ EI là đường trung bình của ΔABD
⇒ EI = AB/2 = 6/2 = 3(cm)
+ ΔABC có CF = BF, CK = AK
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB /2 = 6/2 = 3cm
+ Lại có: EI + IK + KF = EF
⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm

cái này tự vẽ hình
giải: a) hình thang ABCD có: E,F là trung điểm của AD, BC => EF là đường trung bình của hình thang ABCD => EF // CD
xét \(\Delta ADC\) có: E là trung điểm của AD; EK // CD => K là trung điểm của AC => AK = KC
xét \(\Delta DBC\) có: F là trung điểm của BC ; FI // CD => I là trung điểm của DB => BI = ID
b) \(\Delta ADB\) có: E,I là trung điểm của AD, BD => EI là đường trung bình của tam giác ADB => EI = 1/2 . AB = 1/2 . 6 = 3 cm
tương tự ta cũng có KF = 1/2 . AB = 1/2 . 6 = 3 cm
EF là đường trung bình của hình thang ABCD => EF = (AB + CD) / 2 = 16/2 = 8 cm
=> IK = EF - EI - KF = 8 - 3 - 3 = 2 cm
t i c k nhé!!! 5678686798
Gọi a là cạnh của tam giác đều ABC, Slà diện tích của tam giác đều ABC , xlà diện tích tam giác ADB , ylà diện tích tam giác ADC , zlà diện tích tam giác BDC ﴾x,y,z > 0﴿ Ta có : x + y + z = S Mặt khác : x = 2 a.DM ⇒DM = a 2x ; tương tự : DN = a 2y ; DP = a 2z ⇒DM + DN + DP = a 2x + a 2y + a 2z = a 2 x + y + z = a 2S ﴾không đổi﴿ Vậy khi D di chuyển thì DM + DN + DP không đổi ﴾đpcm﴿
ko bít