Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2. 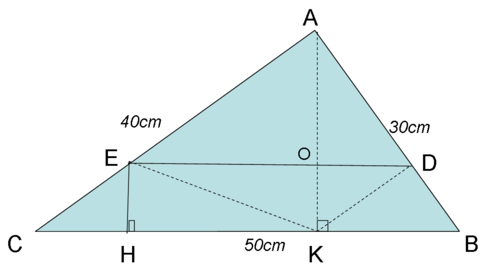
a) Trong tam giác vuông thì 2 cạnh góc vuông cũng chính là 2 đường cao của tam giác đó.
Vậy đường cao AB = 30 cm ; đường cao AC = 40 cm
Đường cao tam giác ABC còn lại đỉnh A là : 30 x 40 : 50 = 24 (cm)
b) S_ECK + S_DKB = CK x 6 : 2 + KB x 6 : 2 = (CK+KB) x 6 : 2 = 50 x 3 = 150 (cm2)
S_AEKD = 30 x 40 : 2 - 150 = 450 (cm2)
Xét tam giác AED và EDK chung đáy ED chiều cao AO = 24 - 6 = 18 (cm)
Tỉ lệ AO/OK = 18/6 = 3. Vậy S_AED = 3 x S_EDK
Diện tích tam giác AED là : 450 : (1+3) x 3 = 337,5 (cm2)

Lời giải:
$BC=\frac{5}{4}AC$
$BC=\frac{5}{3}AB$
$\Rightarrow \frac{5}{4}AC=\frac{5}{3}AB$
$\Rightarrow AC=\frac{5}{3}AB: \frac{5}{4}=\frac{4}{3}AB$
Chu vi tam giác:
$AB+BC+AC=108$
$AB+\frac{5}{3}AB+\frac{4}{3}AB=108$
$AB(1+\frac{5}{3}+\frac{4}{3})=108$
$AB.4=108$
$AB=27$ (cm)
$AC=\frac{4}{3}AB=\frac{4}{3}.27=36$ (cm)
Diện tích tam giác: $AB.AC:2=27.36:2=486$ (cm2)
BL
_ AD định lý Py-ta-go vào \(\Delta ABC\)vuông tại H, ta có:
\(AC^2=AH^2+HC^2\)
\(=>HC^2=AC^2-AH^2\)
\(=>HC^2=4^2-\left(\frac{12}{5}\right)^2\)
\(=>HC^2=\frac{256}{25}\)
\(=>HC=\frac{16}{5}\)( cm)
_ Ta có : \(HB+HC=BC\)
\(=>HB=BC-HC\)
\(=>HB=5-\frac{16}{5}\)
\(=>HB=\frac{9}{5}\)( CM)
_ AD định lý Py-ta-go vào \(\Delta AHB\)vuong tại H, ta có:
\(AB^2=AH^2+HB^2\)
\(=>AB^2=\left(\frac{12}{5}\right)^2+\left(\frac{9}{5}\right)^2\)
\(=>AB^2=9\)
\(=>AB=\sqrt{9}=3\)(cm)
_ Cậu có thể tham khảo bài làm trên đây ạ, chúc cậu học tốt:>