Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

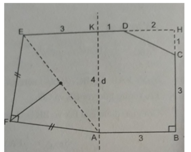
Gọi H là giao điểm của hai đường thẳng ED và BC. Khi đó, ABHE là hình thang và tính được diện tích của nó là
S 1 = 1/2 (AB + EH).BH = 1/2 (3 + 6).4 = 18( c m 2 ).
Diện tích của tam giác vuông DHC là
S 2 = 1/2 DH.CH = 1/2.2.1 = 1( c m 2 ).
Trong tam giác vuông AKE tính được EA = 5 (cm).
Trong tam giác vuông FEA có FE = FA suy ra E F 2 = 25/2.
Từ đó diện tích của tam giác FAE là S 3 = 25/4 c m 2
Vậy diện tích của lục giác đã cho là
S = S 3 + S 1 - S 2 = 25/4 + 18 – 1 = 93/4( c m 2 ).

a. Xét tam giác ABC có:
DE//BC (gt)
=>\(\dfrac{DA}{DB}=\dfrac{EA}{EC}\)(định lý Ta-let) (1)
Xét tam giác ADE có:
AD//CF (gt)
=>\(\dfrac{EA}{EC}=\dfrac{DE}{EF}\)(định lý Ta-let) (2)
Từ (1) và (2) suy ra:\(\dfrac{DA}{DB}=\dfrac{ED}{FE}\)

a) Xét 2∆: ABC và HAB có
+ ∠BAC = 900(gt); ∠BHA = 900 (AH ^ BH) => ∠BAC= ∠BHA
+ ∠ABC = ∠ BAH (so le)
=> ∆ABC ~ ∆HAB
b) Xét 2∆: HAB và KCA có:
+ ∠CKA = 900 (CK ^ AK) => ∠AHB = ∠CKA
+ ∠CAK + ∠BAH = 900(do ∠BAC = 900), ∠BAH + ∠ABH = 900 (∆HAB vuông ở H) =>
∠CAK = ∠ABH
=> ∆HAB ~ ∆KCA
=> AH.AK = BH.CK
c) có: ∆ABC ~ ∆HAB (c/m a)
Ta có: + AH // BC
+ MA + MB = AB => MA + MB = 3cm
=> 34/25MB = 3
=> MB = 75/34cm
+ Diện tích ∆MBC là
S =1/2.AC.MB=75/17

A B C I N M K D E
Có AD // NK, đường tròn (MNK) tiếp xúc với AC tại K, suy ra ^ADM = ^MNK = ^AKM
Suy ra 4 điểm A,M,K,D cùng thuộc một đường tròn. Tương tự với 4 điểm A,M,K,E
Từ đó 5 điểm A,K,M,D,E cùng thuộc một đường tròn
Do vậy ^NDE = ^NKM = ^BNM. Vì 2 góc ^NDE, ^BNM so le trong nên DE // BC hay PQ // BC (đpcm).

a) Xét \(\Delta ABC\) vuông tại A:
\(BC^2=AB^2+AC^2\) (Pytago).
Thay: \(BC^2=3^2+4^2.\)
\(\Rightarrow BC=5\left(cm\right).\)
Xét \(\Delta ABC:\)
BD là đường phân giác (gt).
\(\Rightarrow\dfrac{AD}{CD}=\dfrac{AB}{BC}\) (Tính chất đường phân giác).
\(\Rightarrow\dfrac{AD}{CD+AD}=\dfrac{AB}{BC+AB}.\)
\(\Rightarrow\dfrac{AD}{AC}=\dfrac{AB}{BC+AB}.\)
Thay: \(\dfrac{AD}{4}=\dfrac{3}{5+3}.\)
\(\Rightarrow AD=1,5\left(cm\right).\)
\(\Rightarrow CD=BC-AD=5-1,5=3,5\left(cm\right).\)
b) Xét \(\Delta ABC:\)
DK // AB (gt).
\(\Rightarrow\dfrac{BK}{CK}=\dfrac{AD}{CD}\left(Talet\right).\)
Mà \(\dfrac{AD}{CD}=\dfrac{AB}{BC}\left(cmt\right).\)
\(\Rightarrow\dfrac{BK}{CK}=\dfrac{AB}{BC}.\\ \Rightarrow BK.BC=AB.CK.\)
Gọi H là giao điểm của ED và BC
=> SABHE=\(\dfrac{\left(AB+EH\right).BH}{2}=\dfrac{\left(3+6\right).4}{2}=18\left(cm^2\right)\)
Shình vuông DHC= \(\dfrac{DH.CH}{2}=\dfrac{2.1}{2}=1\left(cm^2\right)\)
Áp dụng định lí Py -ta go trong tam giác vuông EKA
EA=\(\sqrt{EK^2+KA^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
Trong tam giác vuông FEA có FE=FA => \(EF^2=\dfrac{25}{2}\)
=> SFEA=(FE.FA)/2=\(\dfrac{25}{2}:2=\dfrac{25}{4}\left(cm^2\right)\)
vậy S lục giác đã cho = SABHE+ SFEA- Shình vuông DHC=18+\(\dfrac{25}{4}-1=\dfrac{93}{4}\left(cm^2\right)\)
Nhớ tick nha ,đánh quẹo cả tay,em cảm ơn trước ak