Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

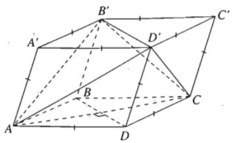
Theo giả thiết các mặt của hình hộp đều là hình thoi.
Ta có ABCD là hình thoi nên AC ⊥ BD
Theo tính chất của hình hộp: BD // B'D', do đó AC ⊥ B'D'.
Chứng minh tương tự ta được AB' ⊥ CD', AD' ⊥ CB'
Hai mặt phẳng (AA'C'C) và (BB'D'D) vuông góc với nhau khi hình hộp ABCD.A'B'C'D'là hình lập phương.

a) Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {a^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Xét tam giác AA’C vuông tại A có
\(A'{C^2} = A{A'^2} + A{C^2} = {a^2} + {\left( {a\sqrt 2 } \right)^2} = 3{a^2} \Rightarrow A'C = a\sqrt 3 \)
Vậy độ dài đường chéo hình lập phương bằng \(a\sqrt 3 \)
b) Ta có \(\begin{array}{l}BD \bot AC,BD \bot AA' \Rightarrow BD \bot \left( {ACC'A'} \right);BD \subset \left( {BDD'B'} \right)\\ \Rightarrow \left( {ACC'A'} \right) \bot \left( {BDD'B'} \right)\end{array}\)
c) Ta có \(C'O \bot BD\left( {BD \bot \left( {ACC'A'} \right)} \right),CO \bot BD \Rightarrow \left[ {C,BD,C'} \right] = \left( {CO,C'O} \right) = \widehat {COC'}\)
\(OC = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác COC’ vuông tại C có
\(\tan \widehat {COC'} = \frac{{CC'}}{{OC}} = \frac{a}{{\frac{{a\sqrt 2 }}{2}}} = \sqrt 2 \Rightarrow \widehat {COC'} = \arctan \sqrt 2 \)
Ta có \(C'O \bot BD\left( {BD \bot \left( {ACC'A'} \right)} \right),AO \bot BD \Rightarrow \left[ {A,BD,C'} \right] = \left( {AO,C'O} \right) = \widehat {AOC'}\)
\(\widehat {AOC'} = {180^0} - \widehat {COC'} \approx 125,{26^0}\)

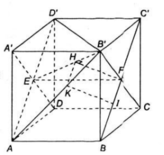

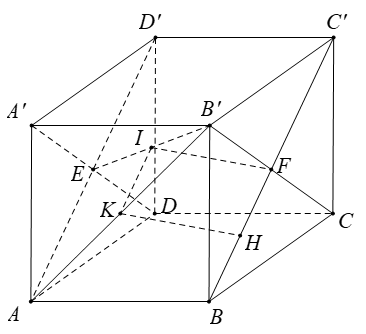
b) Do AD’ // BC’ nên mp(AB’D’) là mặt phẳng chứa AB’ và song song với BC’.
Ta tìm hình chiếu của BC’ trên mp ( AB’D’).
Gọi E và F lần lượt là tâm của các mặt bên ADD’A’ và BCB’C’.

Vậy H là hình chiếu F trên mp (AB’D’). Qua H ta dựng đường thẳng song song với BC’ thì đường thẳng này chính là hình chiếu của BC’ trên mp(AB’D’).
Đường thẳng qua H song song với BC’ cắt AB’ tại K. Qua K kẻ đường thẳng song song với HF, đường này cắt BC’ tại I. Khi đó, KI chính là đường vuông góc chung của AB’ và BC’.


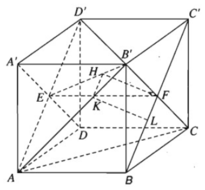
a) Ta có B'C ⊥ BC' vì đây là hai đường chéo của hình vuông BB'C'C
Ngoài ra ta còn có: A'B' ⊥ (BB'C'C) ⇒ A'B' ⊥ BC'
Từ đó ta suy ra BC' ⊥ (A'B'CD) vì mặt phẳng (A'B'CD) chứa đường thẳng A'B' và B'C cùng vuông góc với BC'.
b) Mặt phẳng (AB'D') chứa đường thẳng AB' và song song với BC', ta hãy tìm hình chiếu của BC' trên mặt phẳng (AB'D'). Gọi E, F lần lượt là tâm các hình vuông ADD'A', BCC'B'. Kẻ FH ⊥ EB'với H ∈ EB', khi đó FH nằm trên mặt phẳng (A'B'CD) nên theo câu a) thì FH ⊥ (AB'D'), do đó hình chiếu BC' trên mặt phẳng (AB'D) là đường thẳng đi qua H và song song với BC'. Giả sử đường thẳng đó cắt AB' tại K thì từ K vẽ đường thẳng song song với FH cắt BC' tại L. Khi đó KL là đoạn vuông góc chung cần dựng. Tam giác B'EF vuông tại F nên từ công thức
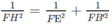
ta tính được
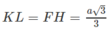
Nhận xét . Độ dài đoạn vuông góc chung của AB' và BC' bằng khoảng cách giữa hai mặt phẳng song song (AB'D') và (BC'D) lần lượt chứa hai đường thẳng đó.
Khoảng cách này bằng 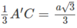

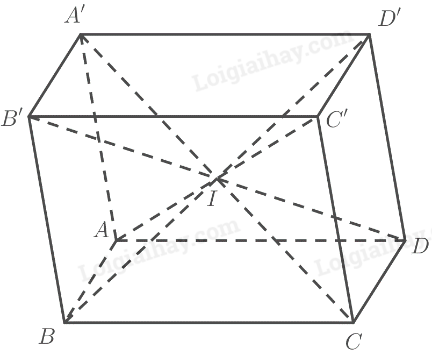
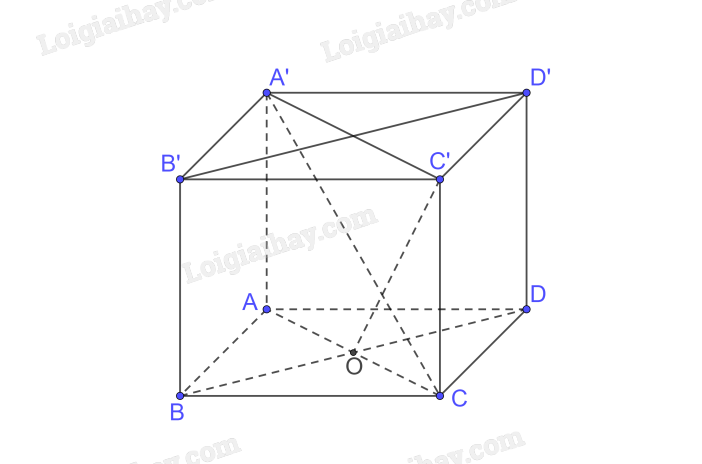
a) Vì \(ABCD.A'B'C'D'\) là hình lăng trụ nên có:
‒ Hai đáy \(ABCD\) và \(A'B'C'D'\) bằng nhau và là hình bình hành.
‒ Các mặt bên \(AA'B'B,AA'D'D,BB'C'C,CC'D'D\) là các hình bình hành.
b) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {AA'C'C} \right) \cap \left( {ABC{\rm{D}}} \right) = AC\\\left( {AA'C'C} \right) \cap \left( {A'B'C'D'} \right) = A'C'\end{array} \right\} \Rightarrow AC\parallel A'C'\)
Mà \(AA'\) và \(CC'\) là các cạnh bên của hình lăng trụ nên \(AA'\parallel CC'\)
Vậy \(AA'C'C\) là hình bình hành.
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {BB'D'D} \right) \cap \left( {ABC{\rm{D}}} \right) = B{\rm{D}}\\\left( {BB'D'D} \right) \cap \left( {A'B'C'D'} \right) = B'D'\end{array} \right\} \Rightarrow B{\rm{D}}\parallel B'D'\)
Mà \(BB'\) và \(DD'\) là các cạnh bên của hình lăng trụ nên \(BB'\parallel DD'\)
Vậy \(BB'D'D\) là hình bình hành.
c) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = C{\rm{D}}\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {A'B'C'D'} \right) = A'B'\end{array} \right\} \Rightarrow C{\rm{D}}\parallel A'B'\left( 1 \right)\)
\(ABC{\rm{D}}\) là hình bình hành nên \(AB = CD\)
\(AA'B'B\) là hình bình hành nên \(AB = A'B'\)
Vậy \(A'B' = CD\left( 2 \right)\)
Từ (1) và (2) suy ra \(A'B'C{\rm{D}}\) là hình bình hành
\( \Rightarrow A'C,B'D\) cắt nhau tại trung điểm của mỗi đường.
Chứng minh tương tự ta có:
+ \(ABC'D'\) là hình bình hành nên \(AC',B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
+ \(A'BCD'\) là hình bình hành nên \(A'C,B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
Do đó bốn đoạn thẳng \(A'C,AC',B'D,BD\) có cùng trung điểm.






Lời giải:
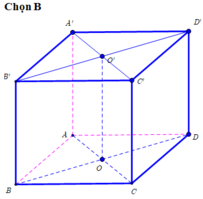
Vì $ABCD.A'B'C'D$ là hình lập phương nên:
$\Rightarrow AC\perp BD; BD\parallel B'D'$
$\Rightarrow AC\perp BD, AC\perp B'D'$
$\Rightarrow AC\perp (BB'D'D)$
Mà $AC\subset (AA'C'C)$ nên $(AA'C'C)\perp (BB'D'D)$
b)
Áp dụng định lý Pitago cho tam giác $DD'O$ vuông tại $D$:
$OD'=\sqrt{DD'^2+DO^2}=\sqrt{DD'^2+(\frac{DB}{2})^2}$
$=\sqrt{DD'^2+(\frac{AD\sqrt{2}}{2})^2}$
$=\sqrt{a^2+(\frac{a\sqrt{2}}{2})^2}=\frac{\sqrt{6}a}{2}$