
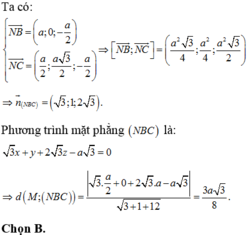
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


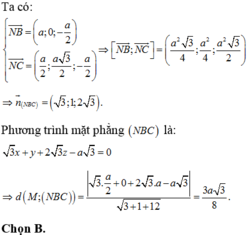

TA CÓ:
= 1+\(\frac{1}{2^2}\)+\(\frac{1}{3^2}\)+.....+\(\frac{1}{49^2}\)+\(\frac{1}{50^2}\)<1+ \(\frac{1}{1\times2}\)+\(\frac{1}{2\times3}\)+....+\(\frac{1}{49\times50}\)
= 1+ 1- \(\frac{1}{2}\) + \(\frac{1}{2}\) - \(\frac{1}{3}\) + ..... + \(\frac{1}{49}\) - \(\frac{1}{50}\)
= 1+ 1 - \(\frac{1}{50}\)
= 1+ \(\frac{49}{50}\) < 2
Chứng tỏ A < 2

Ta có Pt d2 :x+2y-5=0
vì M ϵ d1 :x-y-1=0 nên M(m,m-1)
MA2 = (-1-m)2 + (2-m+1)2 = 1+2m+m2 +9-6m+m2 =2m2 -4m+10
<=> MA=\(\sqrt{2m^2-4m+10}\)
d(m,d2 )= \(\frac{\left|m+2m-2-5\right|}{\sqrt{1^2+2^2}}\) =\(\frac{\left|3m-7\right|}{\sqrt{5}}\)
theo bài ra thì MA=d(M,d2)
=>\(\frac{\left|3m-7\right|}{\sqrt{5}}\)=\(\sqrt{2m^2-4m+10}\) <=>|3m-7|=\(\sqrt{5}\)\(\sqrt{2m^2-4m+10}\)
<=>9m2 -42m +49=5(2m2-4m+10)
<=>9m2 -42m +49=10m2 -20m +50
<=>m2 +22m +1=0
<=>m= -11+2\(\sqrt{30}\) hoặc m=-11-2\(\sqrt{30}\)
=> M(-11+2\(\sqrt{30}\) ,-12+2\(\sqrt{30}\) ) hoặc M(-11-2\(\sqrt{30}\) ,-12-2\(\sqrt{30}\) )

Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)

A B C I 1 2 3 4 5 6
\(I_1+I_2=360^0-90^0-90^0-A=140^0\)
\(I_2=I_3;I_1=I_6\)
\(\Rightarrow I_1+I_2+I_3+I_6=2.140=280^0\)
\(\Rightarrow BIC = 360^0-280^0=80^0\)

a+3c=8 nên c=(8-a)/3
a+2b=9 nên b=(9-a)/2
=>a+3c+a+2b=8+9
2a+2b+2c+c=17
2(a+b+c)=17+c
2[a+(9-a)/2+(8-a)/3]=17+(8-a)/3
2[6a/6+(27-3a)/6+(16-2a)/6]=17+(8-a)/3
2[(6a+27-3a+16-2a)/6]=17+(8-a)/3
2*(a+43)/6=17+(8-a)/3
(a+43)/3-(8-a)/3=17
(a+43-8+a)/3=17
2a+35=17*3=51
2a=51-35
2a=16
a=16/2
a=8
t k chắc, tính nhẩm k cầm mt
Ta có:
a+3c=8 (1)
a+2b=9 (2)
Cộng từng vế các BĐT (1);(2)
=>a+3c+a+2b=8+9
=>(a+a)+3c+2b=17
=>2a+2c+c+2b=17
=>2a+2c+2b+c=17
=>2(a+b+c)+c=17
a+b+c lớn nhất <=>c nhỏ nhất
Mà c >= 0 (do c không âm)
=>c=0
Thay c=0 vào (1) ta có:a+3.0=8=>a+0=8=>a=8
Vậy a=8 thỏa mãn
(*)Linh ak,c từng nói t là super làm dài,bài này thì c cũng đâu khác t đâu? ![]()

a) Ta có:
\(\dfrac{2929-101}{2.2929-404}=\dfrac{29.101-101}{2.29.101-4.101}=\dfrac{101.\left(29-1\right)}{101.\left(2.29-4\right)}=\dfrac{101.28}{101.54}=\dfrac{28}{54}=\dfrac{14}{27}\)
b) Ta có:
\(\dfrac{2.3+4.6+14.21}{3.5+6.10+21.35}=\dfrac{2.3+2.3.2^2+2.3.7^2}{3.5+3.5.2^2+3.5.7^2}=\dfrac{2.3.\left(1+2^2+7^2\right)}{3.5.\left(1+2^2+7^2\right)}=\dfrac{2.3}{3.5}=\dfrac{2}{5}\)