Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(BCC'B'\) là hình chữ nhật \( \Rightarrow BC\parallel B'C'\)
\( \Rightarrow \left( {AB,B'C'} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {60^ \circ }\).
b)
\(\Delta AA'B\) vuông tại \(A \Rightarrow \tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {ABA'} = {45^ \circ }\)
Vậy \(\left( {A'B,\left( {ABC} \right)} \right) = {45^ \circ }\).
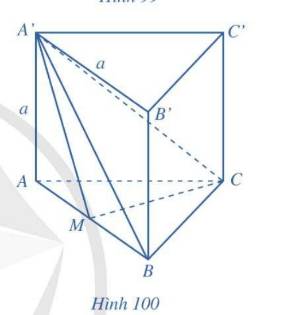
c) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot BC,CC' \bot CM\)
Vậy \(\widehat {BCM}\) là góc nhị diện \(\left[ {B,CC',M} \right]\).
\(\Delta ABC\) đều \( \Rightarrow \widehat {BCM} = \frac{1}{2}\widehat {ACB} = {30^ \circ }\).
d) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right)\)
\(\Delta ABC\) đều \( \Rightarrow CM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\).
\(\left. \begin{array}{l}CC'\parallel AA'\\AA' \subset \left( {ABB'A'} \right)\end{array} \right\} \Rightarrow CC'\parallel \left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC',\left( {ABB'A'} \right)} \right) = d\left( {C,\left( {ABB'A'} \right)} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right) \Rightarrow CM \bot A'M\)
\(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot CM\)
\( \Rightarrow d\left( {CC',A'M} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
g) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4},h = AA' = a\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{4}\)
\({S_{\Delta MBC}} = \frac{1}{2}{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{8},h = AA' = a\)
\( \Rightarrow {V_{A'.MBC}} = \frac{1}{3}{S_{\Delta MBC}}.AA' = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{8}.a = \frac{{{a^3}\sqrt 3 }}{{24}}\)

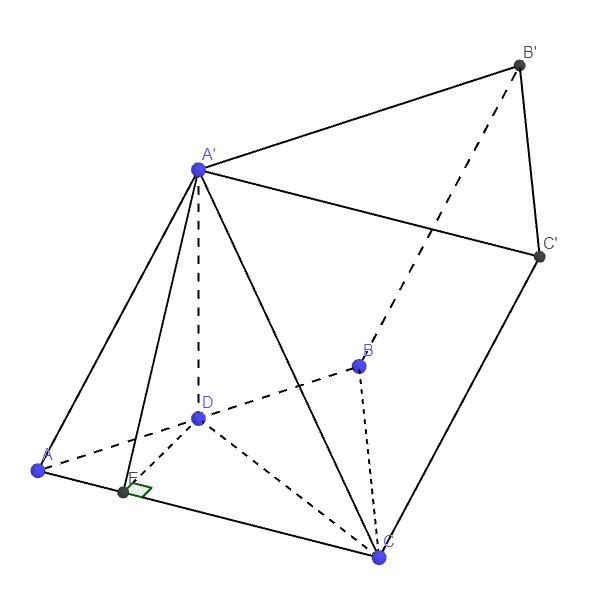
Gọi D là trung điểm AB \(\Rightarrow A'D\perp\left(ABC\right)\)
\(\Rightarrow CD\) là hình chiếu vuông góc của A'C lên (ABC)
\(\Rightarrow\widehat{A'CD}\) là góc giữa A'C và (ABC) \(\Rightarrow\widehat{A'CD}=60^0\)
\(CD=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
\(\Rightarrow A'D=CD.tan60^0=3a\)
Từ D kẻ \(DE\perp AC\) (E thuộc AC)
Mà \(A'D\perp\left(ABC\right)\Rightarrow A'D\perp AC\)
\(\Rightarrow AC\perp\left(A'DE\right)\Rightarrow\widehat{AED}\) là góc giữa (A'AC) và (ABC)
\(DE=AD.sinA=a.sin60^0=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow A'E=\sqrt{A'D^2+DE^2}=\dfrac{a\sqrt{39}}{2}\)
\(\Rightarrow cos\widehat{A'ED}=\dfrac{DE}{A'E}=\dfrac{\sqrt{13}}{13}\)

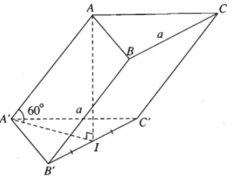
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
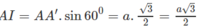
b) 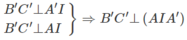
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.

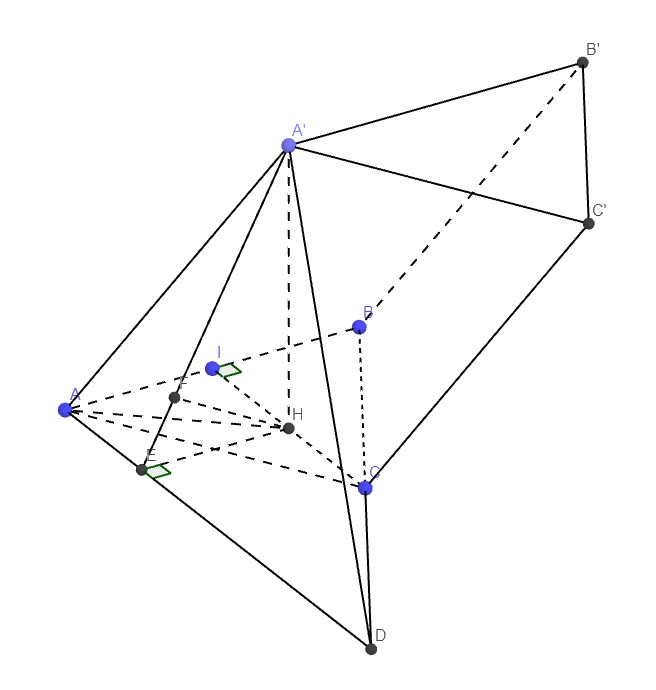
Qua A kẻ đường thẳng song song CI cắt BC kéo dài tại D
\(\Rightarrow CI||\left(A'AD\right)\Rightarrow d\left(A'A;CI\right)=d\left(CI;\left(A'AD\right)\right)=d\left(H;\left(A'AD\right)\right)\)
Từ H kẻ \(HE\perp AD\), từ H kẻ \(HF\perp A'E\)
\(\Rightarrow HF\perp\left(A'AD\right)\Rightarrow HF=d\left(H;\left(A'AD\right)\right)\)
Tứ giác AIHE là hình chữ nhật (3 góc vuông) \(\Rightarrow HE=AI=\dfrac{a}{2}\)
\(A'H\perp\left(ABC\right)\Rightarrow\widehat{A'AH}\) là góc giữa \(A'A\) là (ABC)
\(\Rightarrow\widehat{A'AH}=45^0\)
\(CI=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow IH=\dfrac{1}{2}CI=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow AH=\sqrt{AI^2+IH^2}=\dfrac{a\sqrt{7}}{4}\)
\(\Rightarrow A'H=AH.tan45^0=\dfrac{a\sqrt{7}}{4}\)
Hệ thức lượng:
\(HF=\dfrac{HE.A'H}{\sqrt{HE^2+A'H^2}}=\dfrac{a\sqrt{77}}{22}\)

Đáp án D
Ta có MC là hình chiếu vuông góc của MC’ lên mp (ABC)
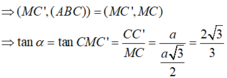
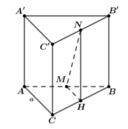
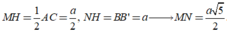
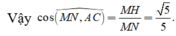


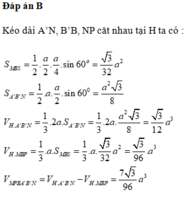
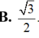
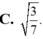
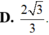
Gọi M là trung điểm BC \(\Rightarrow MG\) là đường trung bình tam giác BCB'
\(\Rightarrow MG||BB'\Rightarrow MG\perp\left(ABC\right)\)
\(\Rightarrow\widehat{GAM}\) là góc giữa AG và (ABC)
\(MG=\dfrac{1}{2}BB'=\dfrac{a}{2}\) ; \(AM=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
\(tan\widehat{GAM}=\dfrac{MG}{AM}=\dfrac{\sqrt{3}}{3}\)