

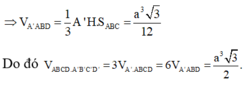
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


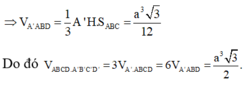

Đặt \(\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{AC}=\overrightarrow{b},\overrightarrow{AA'}=\overrightarrow{c}\)
với \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=0\)
và \(\left|\overrightarrow{a}\right|=a,\overrightarrow{\left|b\right|}=a\sqrt{2},\left|\overrightarrow{c}\right|=a\sqrt{3}\)
khi đó
\(\overrightarrow{AB}=\overrightarrow{a}+\overrightarrow{c,}\overrightarrow{BC}=-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
Giả sử đường vuông góc chung cắt \(\overrightarrow{AB}\) tại M và cắt \(\overrightarrow{BC'}\) tại N và \(\overrightarrow{AM}=x.\overrightarrow{AB'}=x.\overrightarrow{a}+x.\overrightarrow{c},\overrightarrow{BN}=y.\overrightarrow{BC'}=-y.\overrightarrow{a}+y.\overrightarrow{b}+y.\overrightarrow{c}\)
Suy ra \(\overrightarrow{AN}=\left(1-y\right)\overrightarrow{a}+y.\overrightarrow{b}+y.\overrightarrow{c}\)
Và do đó
\(\overrightarrow{MN}=\left(1-x-y\right)\overrightarrow{a}+y.\overrightarrow{b}+\left(y-x\right)\overrightarrow{c}\)
Ta có :
\(MN\perp AB',BC'\Leftrightarrow\begin{cases}\overrightarrow{MN}.\overrightarrow{AB}=0\\\overrightarrow{MN}.\overrightarrow{BC'}=0\end{cases}\)
\(\Leftrightarrow\begin{cases}-4x+2y+1=0\\-2x+6y-1=0\end{cases}\)
Giải hệ ta thu được \(x=\frac{2}{5},y=\frac{3}{10}\)
Từ đó :
\(MN^2=\left[\left(1-x-y\right)^2+2y^2+3\left(y-x\right)^2\right].a^2=\frac{39^a}{100}\)
Suy ra \(d\left(AB';BC'\right)=\frac{a\sqrt{39}}{10}\)