Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

Xem hình cho dễ trả lời nè https://kenh14cdn.com/thumb_w/620/2018/8/31/photo-1-15356853370631011068279.jpg

D A B C N M I G H
\(d\left(M,BN\right)=\frac{\left|13\left(-1\right)-10.2+13\right|}{\sqrt{13^2+10^2}}=\frac{20}{\sqrt{269}}\)
\(H\in\Delta\Leftrightarrow H\left(3a;2a\right)\)
Gọi I là tâm ABCD, G là giao điểm của AC và BN. Ta thấy G là trọng tâm của tam giác BCD
Suy ra \(CG=\frac{2}{3}.CI=\frac{1}{3}AC\) mà \(AM=\frac{1}{4}AC\Rightarrow MG=\frac{5}{12}AC\Rightarrow CG=\frac{4}{5}MG\)
\(\Rightarrow d\left(C,BN\right)=\frac{4}{5}d\left(M,BN\right)=\frac{16}{\sqrt{269}}\Rightarrow d\left(H,BN\right)=2d\left(C,BN\right)=\frac{32}{\sqrt{269}}\)
\(\Leftrightarrow\frac{\left|13.3a-10.2a+13\right|}{\sqrt{269}}=\frac{32}{\sqrt{269}}\Leftrightarrow a=1\) hoặc \(a=\frac{-45}{19}\)
Vì H và M nằm khác phía đối với đường thẳng BN nên \(H\left(3;2\right)\)
Tiếp.........
Ta thấy \(CM=\frac{3AC}{4}=\frac{2AB}{4}=\frac{2CD}{4}=\frac{CD}{2}=CD=CH\Rightarrow\Delta MHN\) vuông tại M
HM có phương trình \(y-2=0\Rightarrow MN:x+1=0\Rightarrow N\left(-1;0\right)\Rightarrow C\left(1;1\right),D\left(-3;-1\right)\)
Do \(\overrightarrow{CM}=3\overrightarrow{MA}\Rightarrow A\left(\frac{-5}{3};\frac{7}{3}\right)\Rightarrow I\left(\frac{-1}{3};\frac{5}{3}\right)\Rightarrow B\left(\frac{7}{3};\frac{13}{3}\right)\)
Vậy \(A\left(\frac{-5}{3};\frac{7}{3}\right);B\left(\frac{7}{3};\frac{13}{3}\right);C\left(1;1\right);D\left(-3.-1\right)\)

A B C D S E K H
Gọi H là trung điểm của AB, suy ra \(SH\perp\left(ACBD\right)\)
Do đó \(SH\perp HD\) ta có :
\(SH=\sqrt{SD^2-DH^2}=\sqrt{SD^2-\left(AH^2+AD^2\right)}=a\)
Suy ra \(V_{s.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{a^2}{3}\)
Gọi K là hình chiếu vuông góc của H trên BD và E là hình chiếu vuông góc của H lên SK. Ta có :
\(\begin{cases}BD\perp HK\\BD\perp SH\end{cases}\) \(\Rightarrow BH\perp\) (SHK)
=> \(BD\perp HE\) mà \(HE\perp SK\) \(\Rightarrow HE\perp\) (SBD)
Ta có : HK=HB.\(\sin\widehat{KBH}\)\(=\frac{a\sqrt{2}}{4}\)
Suy ra \(HE=\frac{HS.HK}{\sqrt{HS^2+HK^2}}=\frac{a}{3}\)
Do đó \(d\left(A:\left(SBD\right)\right)\)=2d(H; (SBD)) =3HE=\(\frac{2a}{3}\)

S o B H A D G d H' C K
Câu a bạn tự tính nhé!
Câu b: Qua G kẻ đường thẳng d // CD , khoảng cách từ \(d\left(G;\left(SAB\right)\right)=d\left(d;\left(SAD\right)\right)\)
Kẻ HH' vuông CD , nối SH'. Lúc này SH' cách d tại K . \(d\left(K;\left(SAB\right)\right)\) là khoảng cách cần tìm.
Ta có: SH'AB =\(\frac{1}{2}S_{ABCD}\)=\(\frac{1}{2}\times2\sqrt{3}a^2=\sqrt{3}a^2\) \(\Rightarrow HH'=\frac{\sqrt{3}a^2}{a}=\sqrt{3}a\)
Vì K nằm trên d nên \(d\left(K;\left(SAB\right)\right)=\frac{2}{3}HH'=\frac{2\sqrt{3}a}{3}\)

A' A B C D H D' C' B'
Tam giác A'AC vuông cân tai A và A'C=a nên A'A=AC=\(\frac{a}{\sqrt{2}}\)
Do đó : \(AB=B'C'=\frac{a}{2}\)
\(V_{ABB'C}=\frac{1}{3}B'C'.S_{\Delta ABB'}=\frac{1}{6}B'C'.AB.BB'=\frac{a^3\sqrt{2}}{48}\)
Gọi H là chân đường cao kẻ từ A của tam giác A'AB. Ta có
\(\begin{cases}AH\perp A'B\\AB\perp BC\end{cases}\)\(\Rightarrow AH\perp\left(A'BC\right)\)
Nghĩa là \(AH\perp\left(BCD'\right)\Rightarrow AH=d\left(A,\left(BCD'\right)\right)\)
Ta có :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AA'^2}\)
Do đó \(d\left(a,\left(BCD'\right)\right)=AH=\frac{a\sqrt{6}}{6}\)



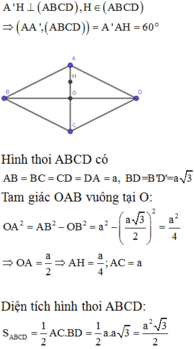


Đáp án C