Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`1,`
S một đáy của hình lập phương đó là:
`144 \div 4 = 36 (m^2)`
Độ dài cạnh của hình lập phương đó là:
\(\sqrt {36} = 6(m)\)
Vậy, độ dài cạnh của hình lập phương đó là `6 m`.
`2,`
P đáy của hình hộp chữ nhật đó là:
`2(5+6)=2*11=22(m^2)`
Chiều cao của hình hộp chữ nhật đó là:
`154 \div 22=7 (m)`
Vậy, độ dài của chiều cao hình hộp chữ nhật đó là `7m.`

Gọi 3 cạnh của hình hộp chữ nhật lần lượt là: x; y; z ( cm; >0)
Diện tích 3 mặt lần lượt là: xy ; yz; xz ( cm^2)
( chú ý hình hộp chữ chữ nhật có 4 cạnh bằng x; 4 cạnh =y; 4 cạnh =z )
Theo bài ra ta có: \(\hept{\begin{cases}\frac{xy}{2}=\frac{yz}{3}=\frac{zx}{5}\left(1\right)\\4x+4y+4z=248\left(2\right)\end{cases}}\)
(1) => \(\frac{x}{2}=\frac{z}{3};\frac{y}{3}=\frac{x}{5}\)=> \(\frac{x}{10}=\frac{z}{15}=\frac{y}{6}\)
(2) => \(x+y+z=62\)
Tự làm tiếp nhé!

Bài 1 : A B C D 4
Vì ABCD là hình vuông \(\Rightarrow\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90^0\)
\(\Rightarrow AB=BC=CD=AD=4\)cm
Áp dụng định lí pytago tam giác ADC vuông tại D ta có :
\(AC^2=AD^2+CD^2=16+16=32\Rightarrow AC=4\sqrt{2}\)cm
Vì ABCD là hình vuông nên 2 đường chéo bằng nhau AC = BD = 4\(\sqrt{2}\)cm
Bài 2 :
A B C D 3 căn27
Vì ABCD là hình chữ nhật nên \(AB=CD;AD=BC\)
Áp dụng định lí Pytago tam giác ACD vuông tại D ta có :
\(AC^2=AD^2+DC^2=27+9=36\Rightarrow AC=6\)cm

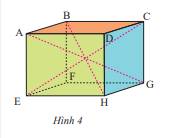
Ta có: AB = DC = EF = HG, mà DC = 5 cm nên AB = 5 cm
AD = BC = FG = EH, mà AD = 8 cm nên FG = 8 cm
AE = FB = DH = CG, mà DH = 6,5 cm nên AE = 6,5 cm

Lời giải:
Diện tích xung quanh của hộp quà:
$2.10(12+8)=400$ (cm2)
Thể tích hộp quà:
$12.8.10=960$ (cm3)

a) Ta có 3 – 2 < 6 < 3 + 2
2cm, 3cm, 6cm không là ba cạnh của tam giác.
b) Vì 6 = 2 + 4
2cm, 4cm, 6cm không là 3 cạnh của một tam giác
c) 4 – 3 < 6 < 4 + 3
3cm, 4cm, 6cm là 3 cạnh của một tam giác.
TK NHA !!!
a) Ta có 3 – 2 < 6 < 3 + 2 bất đẳng thức này sai nên ba độ dài 2cm, 3cm, 6cm không là ba cạnh của tam giác.
b) Vì 6 = 2 + 4 nên ba độ dài là 2cm, 4cm, 6cm không là 3 cạnh của một tam giác
c) 4 – 3 < 6 < 4 + 3 bất đẳng thức đúng nên ba độ dài 3cm, 4cm, 6cm là 3 cạnh của một tam giác.
K NHÉ!!!!!!!

a) Vì 2 + 3 < 6 (trái với bất đẳng thức tam giác) nên 3 độ dài này không thể là 3 cạnh của 1 tam giác.
b) Vì 2 + 4 = 6 (trái với bất đẳng thức tam giác) nên 3 độ dài này không thể là 3 cạnh của 1 tam giác.
c) Vì 3 + 4 > 7 (thỏa mãn bất đẳng thức tam giác) nên 3 độ dài này là 3 cạnh của 1 tam giác
Vẽ hình tam giác có 3 cạnh 3, 4, 7 dùng compa và thước thẳng để vẽ (Tham khảo trong sách giáo khoa)
Chúc học tốt!
Để xác định độ dài các cạnh còn lại của hình hộp chữ nhật ABCD.MNHQ, chúng ta có thể sử dụng định lý Pythagoras. Định lý Pythagoras cho biết rằng trong một tam giác vuông, bình phương của độ dài cạnh huyền bằng tổng bình phương của độ dài hai cạnh góc vuông.
Với hình hộp chữ nhật ABCD.MNHQ, ta có cạnh MN = 6cm, cạnh BC = 4cm và cạnh NB = 3cm. Để xác định độ dài các cạnh còn lại, ta cần tìm độ dài cạnh MH và cạnh NH.
Áp dụng định lý Pythagoras vào tam giác vuông MNH, ta có:
MN^2 = MH^2 + NH^2
Thay các giá trị đã biết vào, ta có:
6^2 = MH^2 + NH^2
36 = MH^2 + NH^2
Để xác định độ dài các cạnh còn lại, chúng ta cần thêm thông tin về tam giác MNH, ví dụ như góc giữa các cạnh.