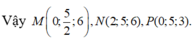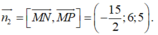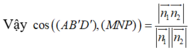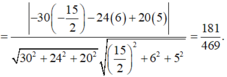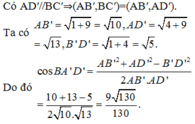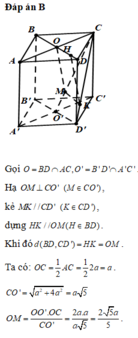Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Đối với những bài cồng kềnh và tính toán rất phức tạp
thế này thì nên tọa độ hóa giải rất nhanh, khỏi phải mất nhiều
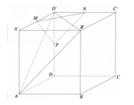
thời gian và tư duy. Gắn trục tọa độ Oxyz như hình vẽ bên với
A'(0;0;0), D(0;5;6), C' (4;5;0)
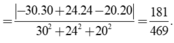
a) Trong (ABCD) kẻ \(CE \bot BD\)
Mà \(CE \bot BB'\left( {BB' \bot \left( {ABCD} \right)} \right) \Rightarrow CE \bot \left( {BB'D'D} \right)\)
Ta có CC’ // BB’ \( \Rightarrow \) CC’ // (BB’D’D) \( \Rightarrow \) d(CC’, (BB’D’D)) = d(C, (BB’D’D)) = CE
Xét tam giác BCD vuông tại C có
\(\frac{1}{{C{E^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{C{D^2}}} = \frac{1}{{{c^2}}} + \frac{1}{{{b^2}}} = \frac{{{b^2} + {c^2}}}{{{c^2}{b^2}}} \Rightarrow CE = \frac{{bc}}{{\sqrt {{b^2} + {c^2}} }}\)
b) \(AC \subset \left( {ABCD} \right),B'D' \subset \left( {A'B'C'D'} \right),\left( {ABCD} \right)//\left( {A'B'C'D'} \right)\)
\( \Rightarrow d\left( {AC,B'D'} \right) = d\left( {\left( {ABCD} \right),\left( {A'B'C'D'} \right)} \right) = BB' = a\)
Đáp án A
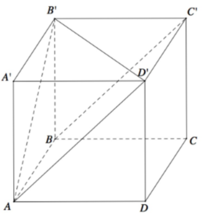
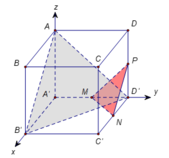
Chọn gốc tọa độ tại D, các tia Ox, Oy, Oz trùng với các tia DC,DA,DD'.
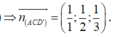
Và B(1;2;0)
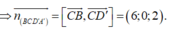
Do đó
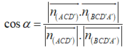
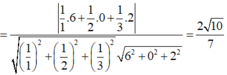
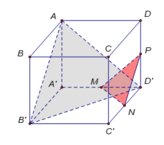
Hai mặt phẳng (AB′D′)(AB′D′) và (A′C′D)(A′C′D) có giao tuyến là EFEF như hình vẽ.
Hai tam giácΔA′C′D=ΔD′AB′ΔA′C′D=ΔD′AB′và EFEF là đường trung bình của hai tam giác nên từ A′A′ và D′D′ ta kẻ 2 đoạn vuông góc lên giao tuyến EFEF sẽ là chung một điểm HH như hình vẽ.
Khi đó, góc giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng A′HA′H và D′HD′H.
Tam giác DEFDEF lần lượt cóD′E=D′B′2=√132D′E=D′B′2=132,D′F=D′A2=52D′F=D′A2=52,EF=B′A2=√5EF=B′A2=5.
Theo hê rông ta có:SDEF=√614SDEF=614. Suy raD′H=2SDEFEF=√30510D′H=2SDEFEF=30510.
Tam giác D′A′HD′A′H có:cosˆA′HD′=HA′2+HD′2−A′D′22HA′.HD′=−2961cosA′HD′^=HA′2+HD′2−A′D′22HA′.HD′=−2961.
Do đóˆA′HD′≈118,4∘A′HD′^≈118,4∘hay(ˆA′H,D′H)≈180∘−118,4∘=61,6∘(A′H,D′H^)≈180∘−118,4∘=61,6∘.
D là hình chiếu vuông góc của D'D′ trên (ABCD)(ABCD).
\Rightarrow \Delta ACD⇒ΔACD là hình chiếu vuông góc của \Delta ACD'ΔACD′ trên mặt phẳng (ABCD)(ABCD).
Do đó \cos \alpha = \dfrac{S_{ACD}}{S_{ACD'}}cosα=SACD′SACD với \alphaα là góc cần tìm.
Ta có \left\{ \begin{aligned} & DA^2 + DC^2 = 3\\ & DC^2 + DD'^2 = 4\\ & DA^2 + DD'^2 = 5\\ \end{aligned}\right. \Leftrightarrow \left\{ \begin{aligned} & DA^2 = 2\\ & DC^2 = 1\\ & DD'^2 = 3\\ \end{aligned}\right.⎩⎪⎪⎨⎪⎪⎧DA2+DC2=3DC2+DD′2=4DA2+DD′2=5⇔⎩⎪⎪⎨⎪⎪⎧DA2=2DC2=1DD′2=3.
\Rightarrow S_{ACD} = \dfrac12.DA.DC = \dfrac{\sqrt2}2⇒SACD=21.DA.DC=22.
Dùng công thức Hê rông ta có S_{ACD'} = \dfrac{\sqrt{11}}2SACD′=211.
Vậy \cos \alpha = \sqrt{\dfrac2{11}}cosα=112.
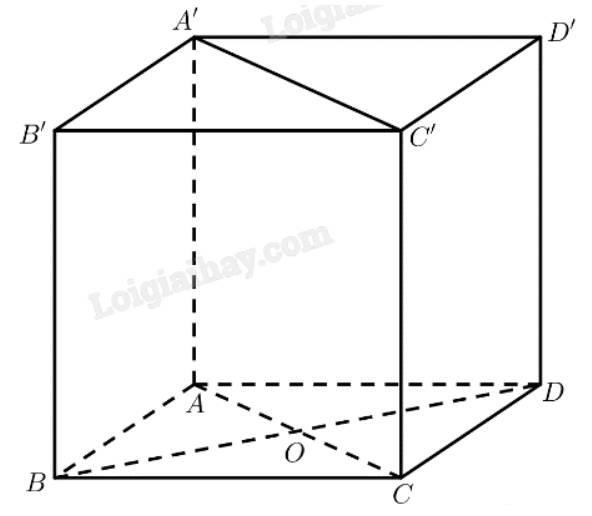
a) Gọi \(O = AC \cap B{\rm{D}}\)
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)
\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
b) Tam giác \(OAB\) vuông tại \(O\)
\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)