Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a/ \(y'=8x-6\)
b/ \(y'=\left(2x-1\right)cosx-sinx\left(x^2-x+2\right)\)
c/ \(y'=\frac{x+2-\left(x-1\right)}{\left(x+2\right)^2}=\frac{3}{\left(x+2\right)^2}\)
d/ \(y'=-\frac{\left(\sqrt{x^2-x-1}\right)'}{x^2-x-1}=-\frac{2x-1}{2\left(x^2-x-1\right)\sqrt{x^2-x-1}}\)
e/ \(y'=\frac{\left[\left(4-3x^2\right)^5\right]'}{2\sqrt{\left(4-3x^2\right)^5}}=\frac{-15x\left(4-3x^2\right)^4}{\sqrt{\left(4-3x^2\right)^5}}=-15x\sqrt{\left(4-3x^2\right)^3}\)
11.
\(SA\perp\left(ABCD\right)\Rightarrow\) AC là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(\Rightarrow\widehat{SCA}=\varphi\)
\(AC=BD=\sqrt{AB^2+AD^2}=a\sqrt{13}\)
\(tan\varphi=\frac{SA}{AC}=\frac{\sqrt{13}}{13}\)
12.
Hai vecto \(\overrightarrow{AB}\) và \(\overrightarrow{EF}\) song song cùng chiều
\(\Rightarrow\left(\overrightarrow{AB};\overrightarrow{EG}\right)=\left(\overrightarrow{EF};\overrightarrow{EG}\right)=\widehat{GEF}=45^0\)
8.
Qua O có 1 và chỉ 1 mặt phẳng vuông góc \(\Delta\)
9.
Gọi O là tâm tam giác BCD
\(\Rightarrow AO\perp\left(BCD\right)\Rightarrow AO\perp CD\)
Mà \(CD\perp BO\) (trung tuyến đồng thời là đường cao)
\(\Rightarrow CD\perp\left(ABO\right)\Rightarrow CD\perp AB\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{CD}=0\)
10.
\(AB\perp AD\Rightarrow\widehat{BAD}=90^0\)
a) Cần biết ít nhật ba trong năm đại lượng u1, n, d, un, Sn thì có thể tính được hai đại lượng còn lại.
b) Thực chất đây là năm bài tập nhỏ, mỗi bài ứng với các dữ liệu ở một dòng. Học sinh phải giải từng bài nhỏ rồi mới điền kết quả.
b1) Biết u1 = -2, un = 55, n = 20. Tìm d, Sn
Áp dụng công thức d =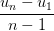 
, Sn =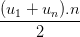 
Đáp số: d = 3, S20 = 530.
b2) Biết d = -4, n = 15, Sn = 120. Tìm u1, un
Áp dụng công thức un = u1 + (n - 1)d và Sn = ,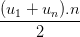
ta có: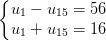 
Giải hệ trên, ta được u1 = 36, u15 = - 20.
Tuy nhiên, nếu sử dụng công thức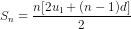 
thì S15 = 120 = 15u1 +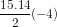 
.
Từ đó ta có u1 = 36 và tìm được u15 = - 20.
b3) Áp dụng công thức un = u1 + (n - 1)d, từ đây ta tìm được n; tiếp theo áp dụng công thức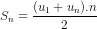 
. Đáp số: n = 28, Sn = 140.
b4) Áp dụng công thức 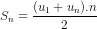, từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: u1 = -5, d= 2.
b5) Áp dụng công thức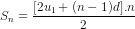 
, từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: n = 10, un = -43
Gọi Q là trung điểm CD \(\Rightarrow EQ//B'C\)
\(\Rightarrow Q\in\left(P\right)\)
Gọi P là trung điểm A'D' \(\Rightarrow EP//B'D'\Rightarrow P\in\left(P\right)\)
Kéo dài EP cắt C'D' kéo dài tại H \(\Rightarrow HC'=\frac{3}{2}C'D'\)
Trong mặt phẳng (CDD'C') nối HQ cắt C'D tại F
Áp dụng định lý talet: \(\frac{FC'}{DF}=\frac{HC'}{DQ}=3\Rightarrow\frac{DC'-DF}{DF}=3\Rightarrow\frac{DC'}{DF}=4\)
3.
\(SA\perp\left(ABC\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABC)
\(AB=\sqrt{AC^2+BC^2}=a\sqrt{3}\)
\(tan\widehat{SBA}=\frac{SA}{AB}=\frac{1}{\sqrt{3}}\Rightarrow\widehat{SBA}=30^0\)
4.
\(f'\left(x\right)=\frac{\left(x^2+3\right)'}{2\sqrt{x^2+3}}=\frac{x}{\sqrt{x^2+3}}\) \(\Rightarrow\left\{{}\begin{matrix}f\left(1\right)=2\\f'\left(1\right)=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow S=2+4.\frac{1}{2}=4\)
5.
Hàm \(y=\frac{3}{x^2+2}\) xác định và liên tục trên R
6.
\(\left\{{}\begin{matrix}k_1=f'\left(2\right)\\k_2=g'\left(2\right)\\k_3=\frac{f'\left(2\right).g\left(2\right)-g'\left(2\right).f\left(2\right)}{g^2\left(2\right)}\end{matrix}\right.\) \(\Rightarrow k_3=\frac{k_1.g\left(2\right)-k_2.f\left(2\right)}{g^2\left(2\right)}\Rightarrow\frac{1}{2}=\frac{g\left(2\right)-f\left(2\right)}{g^2\left(2\right)}\)
\(\Leftrightarrow g^2\left(2\right)=2g\left(2\right)-2f\left(2\right)\)
\(\Leftrightarrow1-2f\left(2\right)=\left[g\left(2\right)-1\right]^2\ge0\)
\(\Rightarrow2f\left(2\right)\le1\Rightarrow f\left(2\right)\le\frac{1}{2}\)
1.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow d\left(C;\left(SAB\right)\right)=BC\)
\(BC=\sqrt{AC^2-AB^2}=a\)
2.
Qua S kẻ đường thẳng d song song AD
Kéo dài AM cắt d tại E \(\Rightarrow SADE\) là hình chữ nhật
\(\Rightarrow DE//SA\Rightarrow ED\perp\left(ABCD\right)\)
\(SBCE\) cũng là hcn \(\Rightarrow SB//CE\Rightarrow SB//\left(ACM\right)\Rightarrow d\left(SB;\left(ACM\right)\right)=d\left(B;\left(ACM\right)\right)\)
Gọi O là tâm đáy, BD cắt (ACM) tại O, mà \(BO=DO\)
\(\Rightarrow d\left(B;\left(ACM\right)\right)=d\left(D;\left(ACM\right)\right)\)
\(\left\{{}\begin{matrix}AC\perp BD\\AC\perp ED\end{matrix}\right.\) \(\Rightarrow AC\perp\left(BDE\right)\)
Từ D kẻ \(DH\perp OE\Rightarrow DH\perp\left(ACM\right)\Rightarrow DH=d\left(D;\left(ACM\right)\right)\)
\(BD=a\sqrt{2}\Rightarrow OD=\frac{1}{2}BD=\frac{a\sqrt{2}}{2}\) ; \(ED=SA=2a\)
\(\frac{1}{DH^2}=\frac{1}{DO^2}+\frac{1}{ED^2}=\frac{9}{4a^2}\Rightarrow DH=\frac{2a}{3}\)
a.
\(cos\left(3x-\frac{\pi}{6}\right)=sin\left(2x+\frac{\pi}{3}\right)\)
\(\Leftrightarrow cos\left(3x-\frac{\pi}{6}\right)=cos\left(\frac{\pi}{6}-2x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\frac{\pi}{6}=\frac{\pi}{6}-2x+k2\pi\\3x-\frac{\pi}{6}=2x-\frac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
b.
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\cos3x\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\cos2x\ne\frac{1}{2}\end{matrix}\right.\)
\(tan3x-tanx=0\)
\(\Leftrightarrow\frac{sin3x}{cos3x}-\frac{sinx}{cosx}=0\)
\(\Leftrightarrow sin3x.cosx-cos3x.sinx=0\)
\(\Leftrightarrow sin2x=0\)
\(\Leftrightarrow2sinx.cosx=0\)
\(\Leftrightarrow sinx=0\Leftrightarrow x=k\pi\)
c.
\(\Leftrightarrow\frac{1}{2}+\frac{1}{2}cos\left(2x-\frac{2\pi}{5}\right)=\frac{1}{2}-\frac{1}{2}cos\left(4x+\frac{8\pi}{5}\right)\)
\(\Leftrightarrow cos\left(2x-\frac{2\pi}{5}\right)=-cos\left(4x+\frac{3\pi}{5}+\pi\right)\)
\(\Leftrightarrow cos\left(2x-\frac{2\pi}{5}\right)=cos\left(4x+\frac{3\pi}{5}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+\frac{3\pi}{5}=2x-\frac{2\pi}{5}+k2\pi\\4x+\frac{3\pi}{5}=\frac{2\pi}{5}-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
d.
\(\Leftrightarrow cos^2\left(2x-1\right)=0\)
\(\Leftrightarrow cos\left(2x-1\right)=0\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{1}{2}+\frac{k\pi}{2}\)
