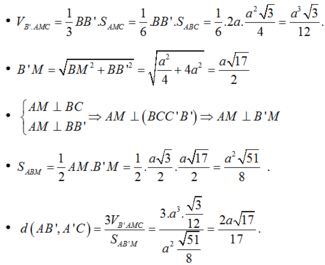Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

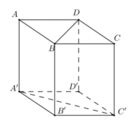
Do SABC là hình chóp đều=>hình chiếu của S lên (ABC) là tâm I củađường tròn ngoại tiếp tam giác ABC=> SI vuông góc với (ABC)
xét tam giác SAI vuông tạị I , biết SA, AI=2/3 AM(là đường cao tgiacs ABC)=> tính được SI
V=1/3. SI.S(ABC)=(căn 11)/12
b) trong (ABC) kẻ hình bình hành AINB
d(AM,SB)=d(AI,SB)=d(I,SBN)( do AI song song AN)=> đưa về tính khoang cách trong tứ diện vuông cơ bản

Chọn A.
Ta có
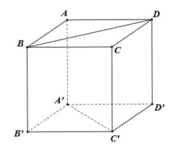
A B C D / / A ' B ' C ' D B D ⊂ A B C D A ' C ' ⊂ A ' B ' C ' D ' ⇒ d B D ; A ' C ' = d A B C D ; A ' B ' C ' D ' = A A ' = a