Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{AC}-\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}\)
Đáp án A đúng

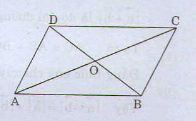
a/ \(\left|\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OB}+\overrightarrow{OD}\right|=\left|\overrightarrow{0}+\overrightarrow{0}\right|=0\)
b/ \(\left|\overrightarrow{OA}+\overrightarrow{OB}\right|+\left|\overrightarrow{OC}+\overrightarrow{OD}\right|=a+a=2a\)
c/
\(\left|\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OB}\right|+\left|\overrightarrow{OD}\right|=\left|\overrightarrow{OB}\right|+\left|\overrightarrow{OD}\right|=2\left|\overrightarrow{OB}\right|=2\sqrt{a^2-\frac{a^2}{4}}=a\sqrt{3}\)