Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD có AE/AB=AH/AD
nên EH//BD và EH=BD/2
Xét ΔCBD có CF/CB=CG/CD
nên FG//BD và FG=BD/2
=>EH//FG và EH=FG
=>EHGF là hình bình hành
Xét ΔBAC cos BE/BA=BF/BC
nên EF//AC và EF=AC/2
=>EF vuông góc với BD
=>EF vuông góc với EH
=>EHGF là hình chữ nhật
b: EH=BD/2=2,5cm
EF=AC/2=4cm
=>\(S_{EFGH}=4\cdot2,5=10\left(cm^2\right)\)

Câu hỏi của Linh Đặng Thị Mỹ - Toán lớp 7 - Học toán với OnlineMath

Kẻ DM ∟ AC sao cho DM = AB.
Dễ dàng chứng minh Δ DMC = Δ AEB (c - g - c)
=> ^DCM = ^AEB và BE = MC (1)
Δ BMD = Δ BED (c - g - c)
=> ^BMD = ^BED và BM = BE (2)
(1) và (2) cho:
^DCM = ^BMD và CM = MB
=> Δ BMC cân tại M
mà ^DMC + ^DCM = 90o (Δ MDC vuông)
=> ^DMC + ^BMD = 90o
=> Δ BMC vuông cân.
=> BCM = 45o
Mà ^ACB + ^DCM = ^BCM
=> ^ACB + ^AEB = 45o (vì ^AEB = ^DCM (cmt))
Cách 2:
Đặt AB = a
ta có: BD = a√2
Do DE/DB = DB/DC = 1/√2
=> Δ DBC đồng dạng Δ DEB (c - g - c)
=> ^DBC = ^DEB
Δ BDC có ^ADB góc ngoài
=> ^ADB = ^DCB + ^DBC
hay ^ACB + ^AEB = 45o
Cách 3
ta có:
tanAEB = AB/AE = 1/2
tanACB = AB/AC = 1/3
tan (AEB + ACB) = (tanAEB + tanACB)/(1 - tanAEB.tanACB)
= (1/2 + 1/3)/(1 - 1/2.1/3) = 1 = tan45o
Vậy ^ACB + ^AEB = 45o
Kẻ DM ∟ AC sao cho DM = AB.
Dễ dàng chứng minh Δ DMC = Δ AEB (c - g - c)
=> ^DCM = ^AEB và BE = MC (1)
Δ BMD = Δ BED (c - g - c)
=> ^BMD = ^BED và BM = BE (2)
(1) và (2) cho:
^DCM = ^BMD và CM = MB
=> Δ BMC cân tại M
mà ^DMC + ^DCM = 90o (Δ MDC vuông)
=> ^DMC + ^BMD = 90o
=> Δ BMC vuông cân.
=> BCM = 45o
Mà ^ACB + ^DCM = ^BCM
=> ^ACB + ^AEB = 45o (vì ^AEB = ^DCM (cmt))
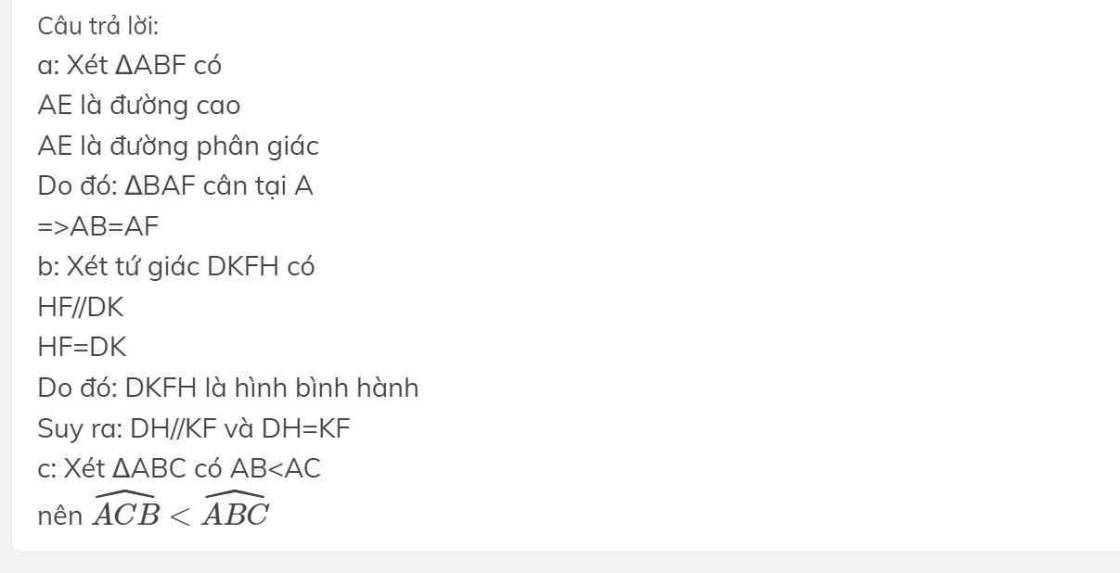
Gọi H′H′ là hình chiếu của H trên BC và G′G′ là hình chiếu của G trên AB.
Ta có: SEFGH=1/2EG.HFSEFGH=1/2EG.HF
Và SABCD=AD.CD;SABCD=AD.CD;
EG≥GG′=AD;EG≥GG′=AD;
HF≥HH′=CD.HF≥HH′=CD.
Do đó: SEFGH≥1/2SABCD.SEFGH≥1/2SABCD.
tk
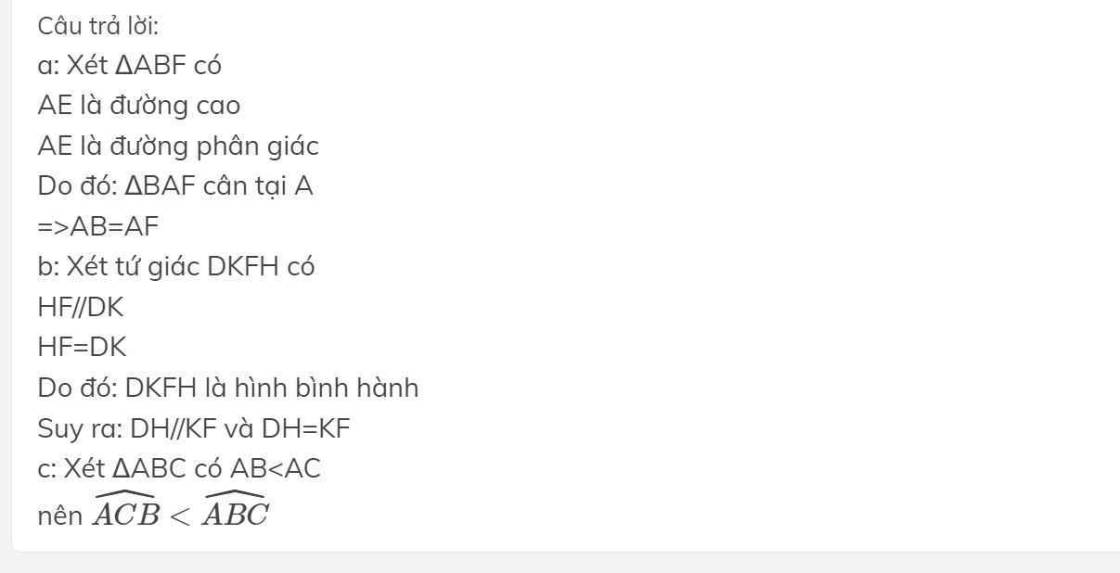
Gọi H′H′ là hình chiếu của H trên BC và G′G′ là hình chiếu của G trên AB.
Ta có: SEFGH=1/2EG.HFSEFGH=1/2EG.HF
Và SABCD=AD.CD;SABCD=AD.CD;
EG≥GG′=AD;EG≥GG′=AD;
HF≥HH′=CD.HF≥HH′=CD.
Do đó: SEFGH≥1/2SABCD.SEFGH≥1/2SABCD.