Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 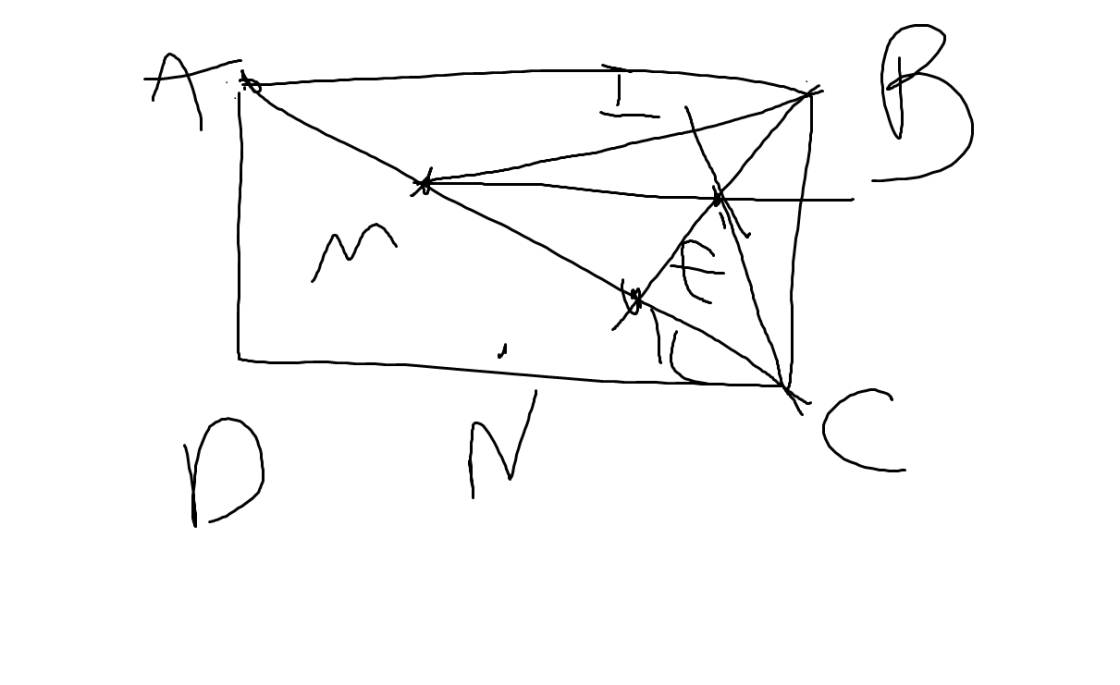
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB

Xét ΔBNC có
CI,BK là đường cao
CI cắt BK tại E
Do đó: E là trực tâm của ΔBNC
=>NE\(\perp\)BC
mà AB\(\perp\) BC
nên NE//AB
Xét ΔKAB có
N là trung điểm của KA
NE//AB
Do đó; E là trung điểm của BK
=>EB=EK

A B C D H M K N E
Gọi N là trung điểm của BH
=> MN là đường trung ình của tam giác ABH
=>MN//AB, MN=1/2 AB
Mà AB=CD và AB//CD
=>MN//CD, MN = 1/2 CD
=> MNCK là hình bình hành
=> NC//MK (1)
Ta có: MN //AB
AB vuông góc với BC
=> MN vuông góc với BC tại E (E thuộc BC)
Tam giác BCM có BH và ME là đường cao và chúng cắt nhau tại N
=> CN vuông góc với BM (2)
Từ (1) và (2) suy ra:
BM vuông góc với MK (đpcm)

Từ K, D hạ đường vuông góc KN, DP xuống AC
Xét tam giác BMK, ta có:
BK^2=BC^2+CK^2 = BC^2+CD^2/4 (1)
BM^2=BH^2+MH^2 = BH^2+ AH^2/4 (2)
MK^2=MN^2+NK^2=MN^2+BH^2/4 (3)
Ta có MN= MH-NH = AH/2-NH=AH/2-(CN-CH)=AH/2-AH/2+CH =CH (Do CN=CP/2=AH/2)
=>MN =CH, thay vào (3)
=> MK^2 = CH^2 +BH^2/4 (4)
Để c/m ^BMK=90o, ta c/m BK^2 =BM^2 +MK^2 (*)
Thay (1), (2), (4) vào (*), , ta được
BC^2+CD^2/4= BH^2+AH^2/4+CH^2+BH^2/4 (**)
Do BC^2= BH^2+CH^2
(**) => CD^2/4= AH^2/4+BH^2/4
=> CD^2=AH^2+BH^2
=> AB^2 = AH^2+BH^2 , đúng do tam giác AHB vuông tại H
Vậy ^BMK =90o
hay BMvuông góc vớ Mk