Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
ABCD là hình thoi
=>AC vuông góc BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại O và O là trung điểm chung của AC và BD
Xét tứ giác OCED có
F là trung điểm chung của OE và CD
Do đó: OCED là hình bình hành
mà góc DOC=90 độ(AC vuông góc BD tại O)
nên OCED là hình chữ nhật
=>DE//OC và DE=OC
=>DE//OA và DE=OA(Do OC=OA)
Xét tứ giác AOED có
AO//ED
AO=ED
Do đó: AOED là hình bình hành
b: Xét tứ giác BDSC có
F là trung điểm chung của DC và BS
Do đó: BDSC là hình bình hành
=>CS//BD
mà CE//BD
và CS cắt CE tại C
nên C,S,E thẳng hàng
c: Để BDSC là hình thoi thì BD=BC
BD=CS(BDSC là hình bình hành)
OD=CE(ODEC là hình chữ nhật)
=>BD=2CE
=>CS=2CE
=>E là trung điểm của CS
=>ES/BD=1/2
Xét ΔKBD và ΔKSE có
góc KBD=góc KSE
góc BKD=góc SKE
Do đó: ΔKBD đồng dạng với ΔKSE
=>KD/KE=BD/SE=2

Có DAB + ABC = 180
Có DAC + CAB = 90 và CBF + FBA = 90
Từ 2 điều trên suy ra FBA + FAB = 90
Xét tam giác ABF có FBA + FAB = 90 (cm trên)
và FBA + FAB + AFB = 180 (3 góc tam giác)
Từ đó suy ra được AFB = 90.
Từ đó biết được đpcm

a) Ta có: \(AF=\dfrac{AD}{2}\)(F là trung điểm của AD)
\(BE=\dfrac{BC}{2}\)(E là trung điểm của BC)
mà AD=BC(Hai cạnh đối trong hình bình hành ABCD)
nên AF=BE
Xét tứ giác AFEB có
AF//BE(AD//BC, F∈AD, E∈BC)
AF=BE(cmt)
Do đó: AFEB là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Ta có: \(AD=2\cdot AB\)(gt)
mà \(AD=2\cdot AF\)(F là trung điểm của AD)
nên AB=AF
Hình bình hành AFEB có AB=AF(cmt)
nên AFEB là hình thoi(Dấu hiệu nhận biết hình thoi)
⇒Hai đường chéo AE và BF vuông góc với nhau tại trung điểm của mỗi đường(Định lí hình thoi)
hay AE⊥BF(đpcm)
b) Ta có: AFEB là hình thoi(cmt)
nên AF=FE=EB=AB và \(\widehat{A}=\widehat{FEB}\)(Số đo của các cạnh và các góc trong hình thoi AFEB)
hay \(\widehat{FEB}=60^0\)
Xét ΔFEB có FE=EB(cmt)
nen ΔFEB cân tại E(Định nghĩa tam giác cân)
Xét ΔFEB cân tại E có \(\widehat{FEB}=60^0\)(cmt)
nên ΔFEB đều(Dấu hiệu nhận biết tam giác cân)
⇒\(\widehat{BFE}=60^0\)(Số đo của một góc trong ΔFEB đều)
Ta có: AB//FE(hai cạnh đối trong hình thoi ABEF)
nên \(\widehat{A}=\widehat{DFE}\)(hai góc đồng vị)
hay \(\widehat{DFE}=60^0\)
Ta có: tia FE nằm giữa hai tia FB,FD
nên \(\widehat{DFB}=\widehat{DFE}+\widehat{BFE}\)
\(\Leftrightarrow\widehat{DFB}=60^0+60^0=120^0\)(1)
Ta có: AD//BC(hai cạnh đối trong hình bình hành ABCD)
nên \(\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía bù nhau)
hay \(\widehat{D}=180^0-60^0=120^0\)(2)
Từ (1) và (2) suy ra \(\widehat{DFB}=\widehat{D}\)
Xét tứ giác BFDC có
FD//BC(AD//BC, F∈AD)
nên BFDC là hình thang có hai đáy là FD và BC(Định nghĩa hình thang)
Hình thang BFDC có \(\widehat{DFB}=\widehat{D}\)(cmt)
nên BFDC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
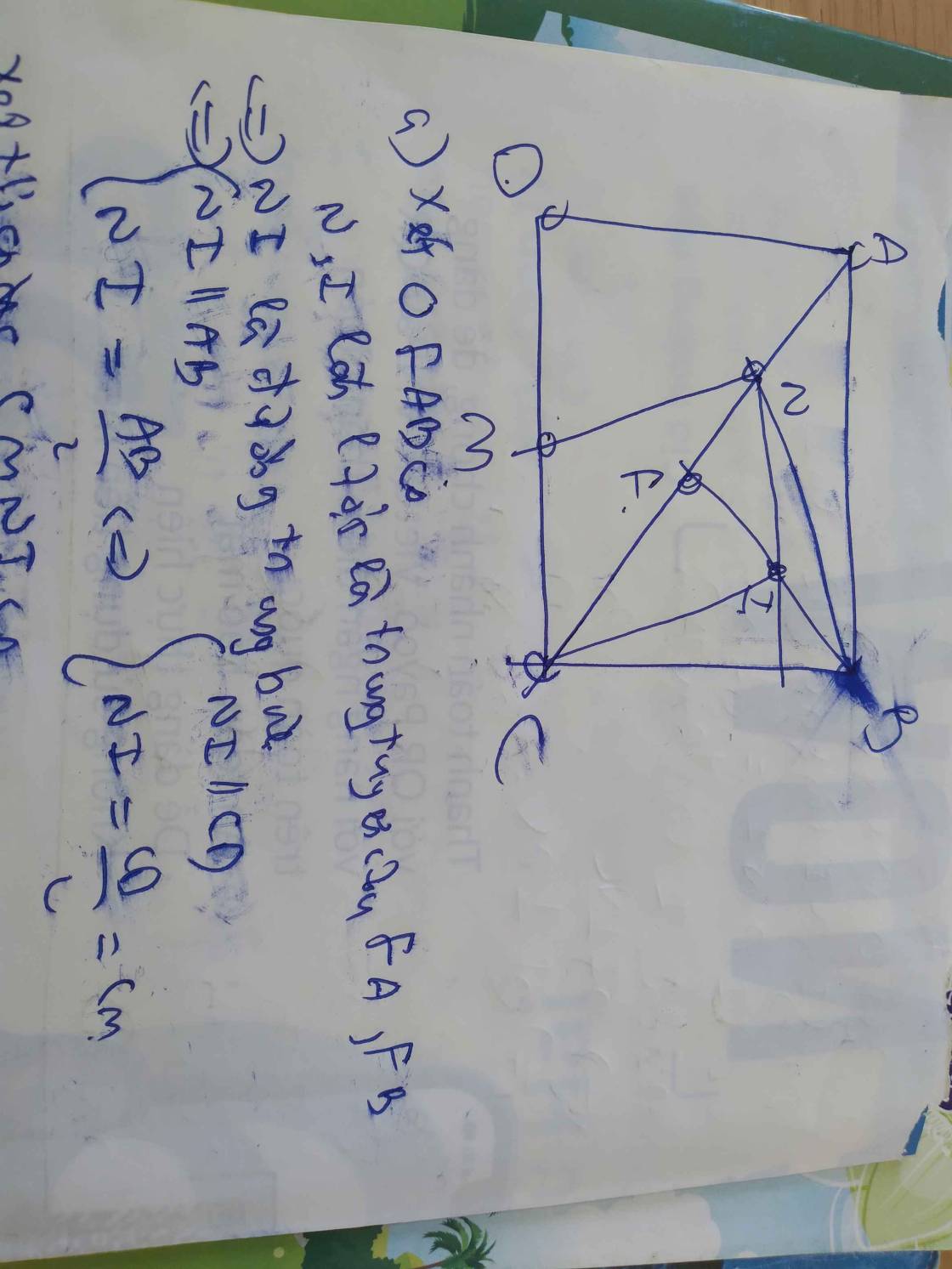


a)Vì A đối xứng với F qua N =>N là trung điểm AF
Mà I là trung điểm BF(gt) => NI là đường trung bình của tam giác FAB
=>NI//AB,NI=1/2AB .Mà AB//CD(ABCD là hình chữ nhật) =>NI//CD hay NI//MC(M thuộc CD) (1)
Vì NI=1/2AB(cmt), AB=CD(ABCD là hcn) => NI=1/2CD
Lại có: M là trung điểm CD(gt) => MC=MD=1/2CD =>NI=MC (2)
Từ (1) và (2) => CINM là hình bình hành
b)Vì NI//CD (cmt), CD vuông góc với BC(ABCD là hình bình hành)
=>NI vuông góc với BC =>NI là đường cao trong tam giác NBC (3)
Vì góc BNM=90 độ(gt) =>BN vuông góc với NM
Lại có :NM//IC(CINM là hình bình hành) =>CI vuông góc với BN
=>CI là đường cao trong tam giác BNC (4)
Từ (3) và (4) =>I là trực tâm trong tam giác BNC =>BI vuông góc với AC hay BF vuông góc với AC