Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho hình thang ABCD có AB//CD, hai đường chéo AC và BD cắt nhau tại O. Chứng ninh rằng OA×OD = OB×OC



Dễ chứng minh \(\Delta ABD=\Delta BAC\) (c.g.c)
\(\Rightarrow\widehat{DBA}=\widehat{CAB}\Rightarrow\Delta OAB\text{ cân tại O}\Rightarrow OA=OB\) (1)
Mặt khác cũng do \(\Delta ABD=\Delta BAC\) suy ra BD = AC hay OB + OD = OA + OC
Do (1) suy ra OD = OC (2)
Nhân theo từng vế hai đẳng thức (1) và (2) ta được đpcm: OA . OD = OB . OC
P/s: Thực ra ban đầu em chẳng có ý tưởng thế này đâu. Nhưng vừa làm xong bài Câu hỏi của Nguyễn Thị Phương Uyên nên mới nghĩ ra hướng chứng minh tương tự thế này đấy ạ:)

a: Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: ˆACD=ˆBDCACD^=BDC^
hay ˆODC=ˆOCDODC^=OCD^
Xét ΔOCD có ˆODC=ˆOCDODC^=OCD^
nên ΔOCD cân tại O
Suy ra: OC=OD
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB

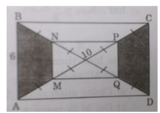
a) Ta có MN và PQ lần lượt là các đường trung bình của các tam giác AOB và COD mà AB // CD và AB = CD nên MN // PQ và MN = PQ
⇒ Tứ giác MNPQ là hình bình hành.
Tương tự NP // BC mà AB ⊥ BC nên MN ⊥ NP. Do đó MNPQ là hình chữ nhật.
Trong ΔABC ta có

Vậy SMNPQ = MN.PQ = 3.4 = 12 (cm2).
b)Dễ thấy ΔAOB = ΔCOD (c.c.c).
Tương tự ΔMON = ΔPOQ
Do đó: SAOB = SCOD và SMON = SPOQ.
⇒ SAOB - SMON = SCOD - SPOQ hay SAMNB = SCPQD.

* Ta có: OA = OB nên tam giác OAB cân tại O
* Do OC = OD nên tam giác OCD cân tại O
* vì OA = OB và OC = OD nên OA + OC = OB + OD
Hay AC = BD
Hình thang ABCD có hai đường chéo AC = BD nên đây là hình thang cân.
Suy ra: BC = AD và B A D ^ = A B C ^ ; A D C ^ = D C B ^
Chọn đáp án D

Câu hỏi của Nguyễn Thị Phương Uyên - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo link trên.

1) Vì ABCD là hình bình hành
=> OA=OC, OB=OD
Ta có: OM=OA/2
OP=OC/2
Mà OA=OC => OM=OP
Cm tương tự ta được OQ=ON
Tứ giác MNPQ có OM=OP. OQ=ON
=> MNPQ là hình bình hành
2) Tứ giác ANCQ có OA=OC (cmt), OQ=ON (cmt)
Suy ra tứ giác ANCQ là hình bình hành
Tứ giác BPDM có OB=OD (cmt), OM=OP (cmt)
Suy ra tứ giác BPDM là hình bình hành

Ta có:
\(OA=OB;OC=OD\)
\(\Rightarrow AC=BD\)
Theo lý thuyết, tứ giác có 2 đường chéo bằng nhau là tứ giác cân
Vậy ABCD là hình thang cân