Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AE = CF (gt)
mà AE // CF (ABCD là hình chữ nhật)
=> AECF là hình bình hành
=> FA // CE
=> AFD = ECF (2 góc đồng vị)
mà ECF = CEB (2 góc so le trong, AB // CD)
=> AFD = CEB (1)
AB = CD (ABCD là hình chữ nhật)
mà AE = CF (gt)
=> AB - AE = CD - CF
=> EB = DF (2)
Xét tam giác NEB và tam giác MFD có:
NEB = MFD (theo 1)
EB = FD (theo 2)
EBN = FDM (2 góc so le trong, AB // CD)
=> Tam giác NEB = Tam giác MFD (g.c.g)
=> BN = DM (2 cạnh tương ứng)
O là trung điểm của BD (3)
=> O là trung điểm của AC (ACBD là hình chữ nhật) (4)
=> O là trung điểm của EF (AECF là hình bình hành) (5)
AEI = ABD (2 góc so le trong, EI // BD)
CFK = CDB (2 góc so le trong, FK // BD)
mà ABD = CBD (2 góc so le trong, AB // CD)
=> AEI = CFK (6)
EI // BD (gt)
FK // DB (gt)
=> EI // FK (7)
Xét tam giác EAI và tam giác FCK có:
IEA = KFC (theo 6)
EA = FC (gt)
EAI = FCK (= 900)
=> Tam giác EAI = Tam giác FCK (g.c.g)
=> EI = FK (2 cạnh tương ứng)
mà EI // FK (theo 7)
=> EIFK là hình bình hành
mà O là trung điểm của EF (theo 5)
=> O là trung điểm của IK (8)
Từ (3), (4), (5) và (8)
=> AC, EF, IK đồng quy tại O là trung điểm của BD
O là trung điểm của AC và BD
=> OA = OC = \(\frac{AC}{2}\)
OB = OD = \(\frac{BD}{2}\)
mà AC = BD (ABCD là hình chữ nhật)
=> OA = OD = OB = OC
=> Tam giác OAD cân tại O
mà AOD = 600
=> Tam giác OAD đều
=> AD = OA = OD
mà AD = 1 cm
AD = BC (ABCD là hình chữ nhật)
=> OA = OD = OC = OB = BC = 1 cm
=> AC = 2OA = 2 . 1 = 2 cm
Xét tam giác BAC vuông tại B có:
\(AC^2=BA^2+BC^2\) (định lý Pytago)
\(AB^2=AC^2-BC^2\)
\(=2^2-1^2\)
\(=4-1\)
= 3
\(AB=\sqrt{3}\)
\(S_{ABCD}=AB\times BC=\sqrt{3}\times1=\sqrt{3}\left(cm^2\right)\)

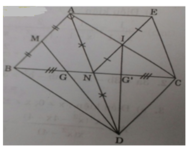
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)

a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình của ΔBAC
Suy ra: EF//AC và \(EF=\dfrac{AC}{2}\left(1\right)\)
Xét ΔADC có
H là trung điểm của AD
G là trung điểm của CD
Do đó: HG là đường trung bình của ΔADC
Suy ra: HG//AC và \(HG=\dfrac{AC}{2}\left(2\right)\)
Từ (1) và (2) suy ra EF//HG và EF=HG
Xét tứ giác EFGH có
EF//HG
EF=HG
Do đó: EFGH là hình bình hành

b) I là tđ của BC => IB=IC=1/2BC=1/2*8=4cm
K_______AD___AK=KA=1/2AD=1/2*8=4cm
do ABCD là hcn =>BC=AD và AD song song BC
=>AK=IC=4cm(=1/2BC=1/2AD)
=>AK song song với IC
=>AICK là hbh
c)bạn tự tính Sabi = Skdc =bao nhiêu tự tính
sau đó tính đc AI=KC=....... (áp dung định lí pi-ta-go vào 2 tam giác trên)
lại xét 2 tam giác AKI = KIC (c.g.c)
sau đó tính diện tích 2 tam giác rồi cộng lại là đk
d) mình cx tịu

a) Tứ giác ����ABCD là hình chữ nhật (GT)
Suy ra ��AD // ��IC (hai cạnh đối) nên tứ giác ����AICD là hình thang.
Mà ���^=90∘ADC=90∘ (góc của hình chữ nhật)
Do đó tứ giác ����AICD là hình thang vuông.
b) Tứ giác ����ABCD là hình chữ nhật nên ��AD // ��,��=��BC,AD=BC.
Mà �I, �K lần lượt là trung điểm của ��BC, ��AD.
Suy ra ��AK // ��IC và ��=��AK=IC.
Tứ giác ����AICK có ��AK // ��IC và ��=��AK=IC nên tứ giác ����AICK là hình bình hành (dấu hiệu nhận biết).
c) Gọi �O là giao điểm của ��AC và ��BD
Suy ra �O là trung điểm của ��AC và ��BD (1) (tính chất đường chéo hình chữ nhật)
Tứ giác ����AICK là hình bình hành (chứng minh trên).
Suy ra ��AC cắt ��IK
Tứ giác ����ABCD là hình chữ nhật (GT)
Suy ra ��AD // ��IC (hai cạnh đối) nên tứ giác ����AICD là hình thang.
Mà ���^=90∘ADC=90∘ (góc của hình chữ nhật)
Do đó tứ giác ����AICD là hình thang vuông.
b) Tứ giác ����ABCD là hình chữ nhật nên ��AD // ��,��=��BC,AD=BC.
Mà �I, �K lần lượt là trung điểm của ��BC, ��AD.
Suy ra ��AK // ��IC và ��=��AK=IC.
Tứ giác ����AICK có ��AK // ��IC và ��=��AK=IC nên tứ giác ����AICK là hình bình hành (dấu hiệu nhận biết).
c) Gọi �O là giao điểm của ��AC và ��BD
Suy ra �O là trung điểm của ��AC và ��BD (1) (tính chất đường chéo hình chữ nhật)
Tứ giác ����AICK là hình bình hành (chứng minh trên).
Suy ra ��AC cắt ��IK
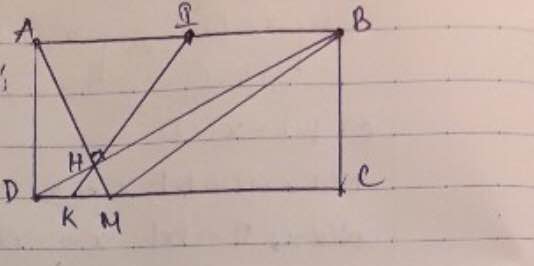

a: BI=6/2=3cm
=>\(AI=\sqrt{8^2+3^2}=\sqrt{73}\left(cm\right)\)
\(S_{AICK}=\sqrt{73}\cdot3\left(cm^2\right)\)
b: AICK là hình bình hành
=>AC cắt IK tại trung điểm của mỗi đường(1)
ABCD là hbh
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra AC,IK,BD đồng quy