Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

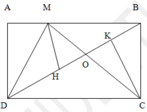
a. Nối M vơi D. Ta có S M D C = S B D C (Vì chung đay DC và chiều cao bằng chiều rộng hình chữ nhật).
Hai tam giác MDC và BDC có chung phần S O D C và có diện tích bằng nhau nên: S M D O = S B O C
b. Diện tích hình chữ nhật ABCD là ABCD
6 x 4 = 24 ( c m 2 )
Diện tích hình tam giác ADM là:
24 – 20 = 4 ( c m 2 )
Độ dài đoạn MA là:
4 x 2 : 4 = 2 ( cm )
c. Độ dài MB là:
6 – 2 = 4 ( cm )
S D M B = 2 3 S B D C (Vì đáy MB = 2 3 DC và chiều cao bằng chiều rộng của hình chữ nhật. )
Nếu coi M và C là đỉnh. Hai tam giác MBD và CBD có chung đáy BD và S M B D = 2 3 S B D C suy ra chiều cao MH = + 2 3 CK
Hai tam giác MDO và CDO có chung đáy DO và chiều cap MH = 2 3 CK
Suy ra S M D O = 2 3 S C D O

Bạn thích thì vẽ, không vẽ cũng không sao, bài này mình cho mấy bạn Ôn thi vào lớp 6 tham khảo ...

đoạn thẳng AM là
12.\(\frac{1}{3}\)=4( cm)
đoạn thẳng DN là
6.\(\frac{2}{3}\)= 4(cm)
hok tốt
đoạn thẳng AM là
12.\(\frac{1}{3}\)=4( cm)
đoạn thẳng DN là
6.\(\frac{2}{3}\)= 4(cm)
hok tốt

a/
\(S_{ABC}=\frac{1}{2}xABxAC=\frac{30x40}{2}=600cm^2\)
\(S_{ABC}=\frac{1}{2}xBCx\)đường cao hạ Từ A->BC \(=\frac{50}{2}x\) đường cao hạ Từ A->BC \(=600cm^2\)
=> đường cao hạ từ A->BC = 2x600:50=24 cm
b/
\(AE=\frac{AC}{3}\Rightarrow\frac{AE}{AC}=\frac{1}{3}\Rightarrow\frac{AE}{CE}=\frac{1}{2}\)
Xét tg ABE và tg BCE có chung đường cao hạ từ B->AC nên
\(\frac{S_{ABE}}{S_{BCE}}=\frac{AE}{CE}=\frac{1}{2}\Rightarrow S_{ABE}=\frac{S_{BCE}}{2}\Rightarrow S_{BCE}=2xS_{ABE}\)
\(S_{ABE}+S_{BCE}=S_{ABE}+2xS_{ABE}=3xS_{ABE}=S_{ABC}=600cm^2\Rightarrow S_{ABE}=200cm^2\)
Xét tg BDE và tg BCE có chung đường cao hạ từ E->BC nên
\(\frac{S_{BDE}}{S_{BCE}}=\frac{BD}{BC}=\frac{1}{2}\Rightarrow S_{BDE}=\frac{S_{BCE}}{2}\)
\(\Rightarrow S_{ABE}=S_{BDE}=200cm^2\) Hai tg này có chung BE nên đường cao hạ từ A->BE = đường cao hạ từ D->BE
Xét tg ABD và tg ABC có chung đường cao hạ từ A->BC nên
\(\frac{S_{ABD}}{S_{ABC}}=\frac{BD}{BC}=\frac{1}{2}\Rightarrow S_{ABD}=\frac{S_{ABC}}{2}\)
Xét tg ABM và tg BDM có chung BM nên
\(\frac{S_{ABM}}{S_{BDM}}=\)đường cao hạ từ A->BE / đường cao hạ từ D->BE = 1 \(\Rightarrow S_{ABM}=S_{BDM}\)
Mà \(S_{ABM}+S_{BDM}=S_{ABD}=2xS_{ABM}\Rightarrow S_{ABM}=\frac{S_{ABD}}{2}=\frac{S_{ABC}}{4}=\frac{600}{4}=150cm^2\)
Ta có \(S_{AME}=S_{ABE}-S_{ABM}=200-150=50cm^2\)
c/ Từ kết quả câu (b) ta có \(S_{ABM}=S_{ADM}\) Hai tg này có chung đường cao hạ từ B->AD nên
\(\frac{S_{ABM}}{S_{BDM}}=\frac{AM}{MD}=1\Rightarrow AM=MD\)
a) Nối M vơi D. Ta có S MDC = S BDC (Vì chung đay DC và chiều cao bằng chiều rộng hình chữ nhật).
Hai tam giác MDC và BDC có chung phần S ODC và có diện tích bằng nhau nên:
S MDO = S BOC
b) Diện tích hình chữ nhật ABCD là ABCD
6 x 4 = 24 ( cm2)
Diện tích hình tam giác ADM là: 4 – 20 = 4 ( cm2)
Độ dài đoạn MA là: 4 x 2 : 4 = 2 ( cm )
c) Độ dài MB là:6 – 2 = 4 ( cm )
S DMB = 2/3 S BDC (Vì đáy MB = 2/3 DC và chiều cao bằng chiều rộng của hình chữ nhật. )
Nếu coi M và C là đỉnh. Hai tam giác MBD và CBD có chung đáy BD và SMBD = 2/3 SBDC suy ra chiều cao MH = + 2/3 CK
Hai tam giác MDO và CDO có chung đáy DO và chiều cap MH = 2/3 CK
Suy ra SMDO = 2/3 SCDO