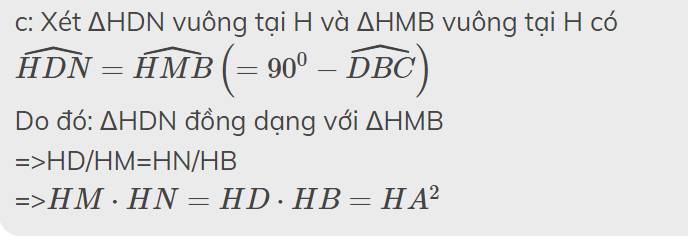KA
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 10 2023
a: ΔABD vuông tại A
=>\(BD^2=AB^2+AD^2\)
=>\(BD^2=9^2+12^2=225\)
=>BD=15(cm)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH\cdot BD=AB\cdot AD\)
=>\(AH\cdot15=12\cdot9=108\)
=>AH=108/15=7,2(cm)
XétΔABD vuông tại A có \(sinBDA=\dfrac{AB}{BD}=\dfrac{9}{15}=\dfrac{3}{5}\)
nên \(\widehat{BDA}\simeq37^0\)
b: Xét ΔAHB vuông tại H có HI là đường cao
nên \(AI\cdot AB=AH^2\left(1\right)\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\left(2\right)\)
Từ (1) và (2) suy ra \(AI\cdot AB=HD\cdot HB\)
c: Xét ΔHDN vuông tại H và ΔHMB vuông tại H có
\(\widehat{HDN}=\widehat{HMB}\left(=90^0-\widehat{DBC}\right)\)
Do đó: ΔHDN đồng dạng với ΔHMB
=>HD/HM=HN/HB
=>\(HM\cdot HN=HD\cdot HB=HA^2\)
21 tháng 8 2021
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABD vuông tại A có AH là đường cao ứng với cạnh huyền BD, ta được:
\(AH^2=HB\cdot HD\left(1\right)\)
Ta có: \(\widehat{HDN}=\widehat{HBA}\)
\(\widehat{HMB}=\widehat{HBA}\left(=90^0-\widehat{BAH}\right)\)
Do đó: \(\widehat{HDN}=\widehat{HMB}\)
Xét ΔHDN vuông tại H và ΔHMB vuông tại H có
\(\widehat{HDN}=\widehat{HMB}\)
Do đó: ΔHDN\(\sim\)ΔHMB
Suy ra: \(\dfrac{HD}{HM}=\dfrac{HN}{HB}\)
hay \(HD\cdot HB=HM\cdot HN\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(HA^2=HM\cdot HN\)
DT
Đỗ Thanh Hải
CTVVIP
22 tháng 9 2021
Hình tự vẽ nha bạn
Xét tam giác ABD vuông tại A (ABCD là hình chứ nhật nên góc A = 90 độ)
Áp dụng hệ thức lượng trong tam giác vuông
\(\dfrac{1}{AD^2}+\dfrac{1}{AB^2}=\dfrac{1}{AH^2}\)
Thay số vào tính được AD = 15cm
Chu vi HCN = (20+15).2 = 70cm
H
22 tháng 9 2021
Xét tam giác AHB vuông tại H có
\(AH^2+HB^2=AB^2\)( đl PYtago)
T/s \(12^2+HB^2=20^2\)
=>\(HB^2=20^2-12^2\)
=> \(HB^2=256\)
=> \(HB=16\)
Xét tam giác DAB vuông tại A có
\(AH^2=DH.HB\)
⇔ \(12^2=DH.16\)
=> \(DH=24\)
Xét tam giác AHD vuong tại H có
\(AH^2+DH^2=AD^2\)( đl Pyta go)
T/s \(12^2+24^2=AD^2\)
=> AD = \(12\sqrt{5}\)
Chu vi HCN ABCD là
( AB + AD ).2
= ( 20 +12\(\sqrt{5}\)).2
= 93,6 cm
Vây chu vi là 93,6 cm
3 tháng 5 2022
a) tam giác ABC vuông tại A => AB2 + AC2 = BC2 ( định lý py-ta-go)
hay 92 + 122 = BC2
=> BC2 = 81 + 144 = 225 => BC = √225=15cm225=15cm
trong tam giác ABC có: AB < AC < BC
=> góc C < góc B < góc A (định lý)