Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABH và ΔACB có:
∠BHA = ∠CBA = 90o
∠BAH = ∠CAB (góc chung)
⇒ Hai tam giác đồng dạng
⇒ BA/CA = AB/AH
⇒ AB2 = AC.AH
Xét ΔABH vuông tại H và ΔACB vuông tại B có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACB
Suy ra: \(\dfrac{AB}{AC}=\dfrac{AH}{AB}\)
hay \(AB^2=AC\cdot AH\)

a: ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(AC^2=4^2+3^2=25\)
=>AC=5(cm)
Xét ΔBAC vuông tại B có BH là đường cao
nên \(BH\cdot AC=BA\cdot BC\)
=>BH*5=3*4=12
=>BH=2,4(cm)
Xét ΔBAC vuông tại B có
\(sinBAC=\dfrac{BC}{AC}=\dfrac{3}{5}\)
=>\(\widehat{BAC}\simeq37^0\)
b: Xét ΔABE vuông tại A có AH là đường cao
nên \(BH\cdot BE=BA^2\)(1)
Xét ΔABC vuông tại B có BH là đường cao
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)
c: Xét ΔBHC vuông tại H và ΔBFE vuông tại F có
\(\widehat{HBC}\) chung
Do đó: ΔBHC\(\sim\)ΔBFE
=>\(\dfrac{BH}{BF}=\dfrac{BC}{BE}\)
=>\(\dfrac{BH}{BC}=\dfrac{BF}{BE}\)
Xét ΔBHF và ΔBCE có
BH/BC=BF/BE
\(\widehat{HBF}\) chung
Do đó: ΔBHF\(\sim\)ΔBCE

a: BC=căn 6^2+8^2=10cm
BH=AB^2/BC=3,6cm
CH=10-3,6=6,4cm
sin ABC=AC/BC=4/5
=>góc ABC=53 độ
b: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
c: góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật
góc KAC+góc AFE
=góc AHE+góc KCA
=góc ABC+góc ACB=90 độ
=>AK vuông góc EF

2)
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow DE^2=2\cdot4.5=9\)
hay DE=3(cm)
b) Xét ΔABH vuông tại H có
\(\tan\widehat{ABC}=\dfrac{AH}{HB}=\dfrac{3}{2}\)
nên \(\widehat{ABC}\simeq56^0\)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot5=3\cdot4=12\)
hay AH=2,4cm

bài 9
tam giác ABC vuông tại A có
* BC2=AB2+AC2
BC2=152+202=625
BC=25cm
* AH.BC=AB.AC
AH.25=15.20
AH.25=300
AH=12cm
tam giác ABH vuông tại H có
BH2=AB2-AH2
BH2=152-122=81
BH=9cm
tam giác ABC vuông tại A có
*AB2=BH.BC
225=9.BC
BC=25cm
CH=BC-BH=25-9=16cm
*AC2=BC2-AB2
AC2=252-152=400
AC=20cm

Hình bạn tự vẽ nha :v
a, áp dụng định lý pytago vào tam giác ABC có góc BAC =90 ta đc : BC2=AC2+AB2 thay vào là đc nha
áp dụng hệ thức lượng vào tam giác ABC có góc BAC=90 ta dc :AH.BC=AB.AC thay vào là đc nha
Mà AM=1/2 BC thay vào nha :v
b, Xét tam giác ABE và tam giác ABF có : góc ABF - góc chung và góc AEB= góc BAF=90 => tam giác ABE đồng dạng tam giác FBA => BE/BA=AB/FB=> BE.FB=AB2(1)
áp dụng hệ thức lượng vào tam giác ABC có góc BAC=90 ta đc : AB2 =BH.BC(2)
từ (1) và (2) => dpcm
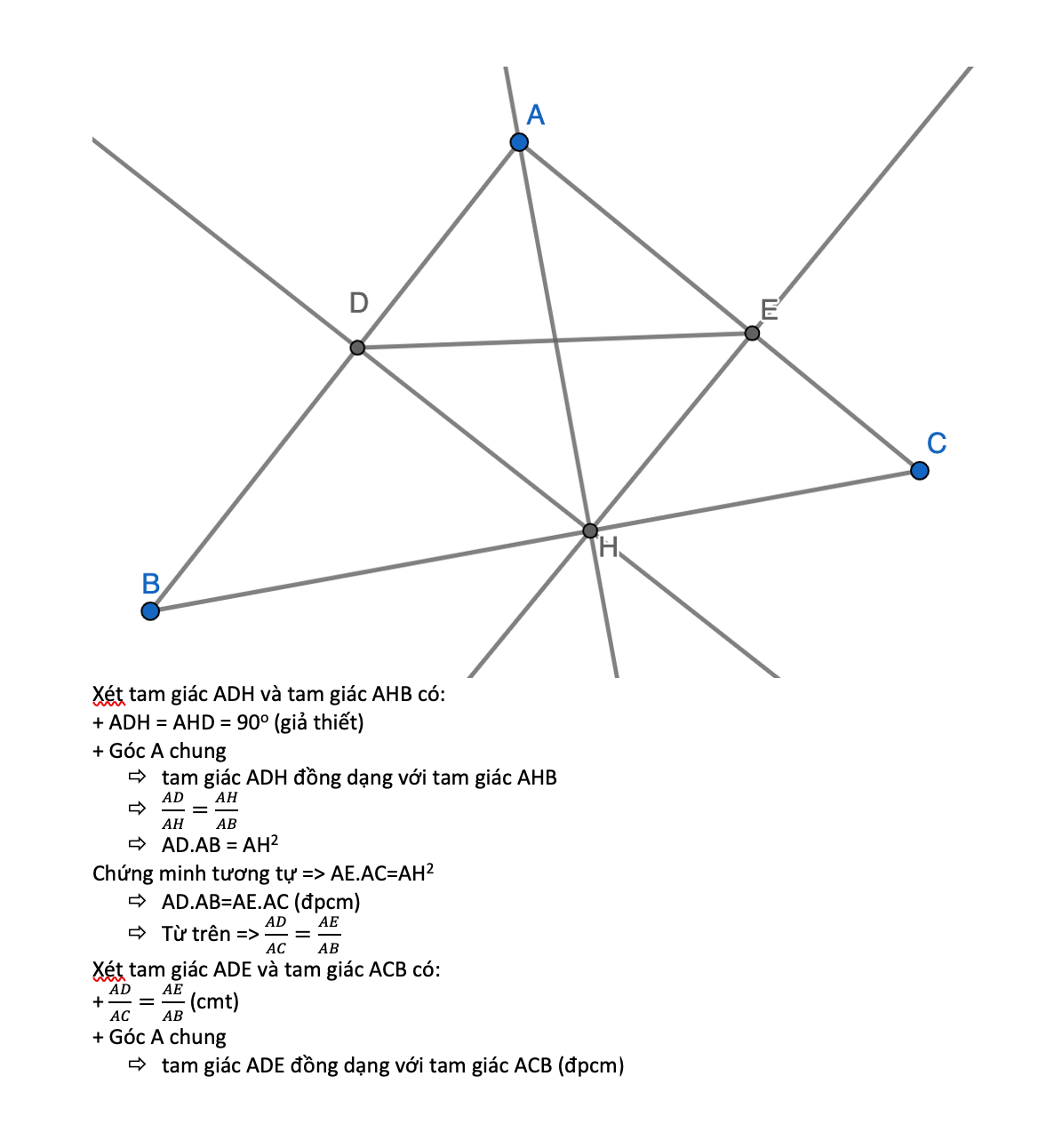
a: Xét ΔABH vuông tại H và ΔACB vuông tại A có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACB
Suy ra: \(\dfrac{AB}{AC}=\dfrac{AH}{AB}\)
hay \(AC\cdot AH=AB^2\)