Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

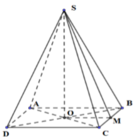
Gọi M là trung điểm của BC. Ta có: O M ⊥ B C S O ⊥ B C ⇒ B C ( S O M )
⇒ B C ⊥ S M
Ta có:
S B C ⊥ A B C D = B C S S B C ⊃ S M ⊥ B C ( A B C D ) ⊃ O M ⊥ B C ⇒ ∠ S B C , A B C D = ∠ S M ; O M = ∠ S M O
ABCD là hình vuông cạnh a ⇒ O B = 1 2 B D = a 2 2
∆ S O B vuông tại O ⇒ S O = S B 2 - O B 2
= a 2 - a 2 2 = a 2 2
O M = A B 2 = a 2 . ∆ S O M vuông tại O
⇒ tan S M O = S O O M = a 2 2 a 2 = 2
Vậy, cos ∠ S B C , A B C D = 1 3
Chọn đáp án A.

Đáp án A
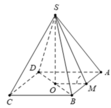
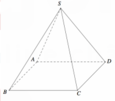
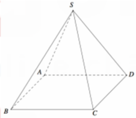
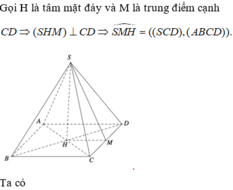
Xét hình chóp tứ giác đều S.ABCD có các cạnh bằng a.
Gọi O là tâm hình vuông ABCD, M là trung điểm của AB.
Khi đó S O ⊥ A B O M ⊥ A B ⇒ A B ⊥ S M O ⇒ S A B ; A B C D ^ = S M O ^
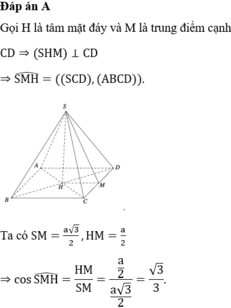
Tam giác SMO vuông tại O, có c o s S M O ^ = O M S M = a 2 : a 3 2 = 3 3
Vậy c o s S A B ; A B C D ^ = 3 3

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

ta có \(y=\frac{3\left(x+1\right)}{x-2}=3+\frac{9}{x-2}\) để các điểm trên C có tọa độ nguyên thì (x,y) nguyên
suy ra (x-2) là ước của 9
mà \(Ư\left\{9\right\}=\left\{\pm9;\pm3;\pm1\right\}\)
TH1: x-2=-9 suy ra x=-7 suy ra y=3-1=2
th2: x-2=9 suy ra x=11 suy ra y=3+1=4
th3:x-2=-3 suy ra x=-2 suy ra y=3-3=0
th4: x-2=3 suy ra x=5 suy ra y=3+3=6
th5:x-2=1 suy ra x=3 suy ra y=3+9=12
th6: x-2=-1 suy ra x=1 suy ra y=3-9=-6
kết luận....
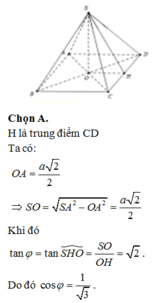

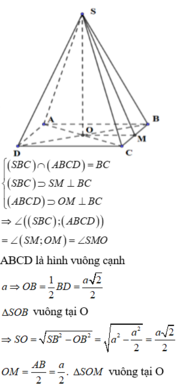
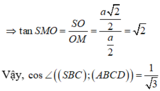


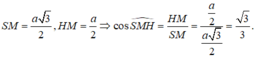
Đáp án là A