Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Cách xác định tâm mặt cầu ngoại tiếp khối chóp:
- Xác định tâm O của đường tròn ngoại tiếp đa giác đáy
- Từ O dựng đường thẳng d vuông góc với mặt phẳng đáy
- Dựng mặt phẳng trung trực α của một cạnh bên nào đó
- Xác định I = α ∩ d I chính là tâm mặt cầu ngoại tiếp hình chóp đã cho
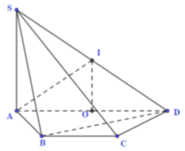


Đáp án A
Phương pháp:
Xác định tâm đường tròn ngoại tiếp hình chóp
- Xác định tâm O đường tròn ngoại tiếp đa giác đáy.
- Vẽ đường thẳng (d) qua O và vuông góc đáy.
- Vẽ mặt phẳng trung trực của một cạnh bên bất kì cắt (d) tại I chính là tâm mặt cầu ngoại tiếp cần tìm và bán kính R = IA = IB =IC = …
Cách giải:
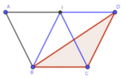
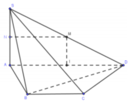
ABCD là hình thang cân => ABCD là tứ giác nội tiếp => Đường tròn ngoại tiếp tam giác BCD trùng với đường tròn ngoại tiếp hình thang ABCD.
Gọi I là trung điểm AD. Do AB = CD = BC = a, AD = 2a, ta dễ dàng chứng minh được I là tâm đường tròn ngoại tiếp ABCD => I là tâm đường tròn ngoại tiếp tam giác BCD.
Gọi M, N lần lượt là trung điểm của SD, SA.
Þ MI, MN là các đường trung bình của tam giác SAD
Þ MI//SA, MN//AD
Mà 
Þ MB = MC = MD = MA, MN là trung trực của SA
Þ MB = MC = MD = MS (=MA)
Þ M là tâm khối cầu ngoại tiếp hình chóp S.BCD
Bán kính

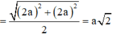
Thể tích mặt cầu:
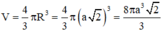

Đáp án B
Diện tích hình thang ABCD là:
S A B C D = A B . A D + B C 2 = 5
Vậy thể tích khối chóp S.ABCD là:
V = 1 3 . S A . S A B C D = 1 3 . S A . S A B C D = 1 3 .2.5 = 10 3 (đvtt)

Đáp án A.
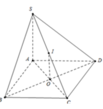
Do ABCD là hình chữ nhật nên khối cầu ngoại tiếp hình chóp S.BCD chính là khối cầu ngoại tiếp hình chóp S.ABCD
Khi đó
R = S C 2 = S A 2 + A B 2 + A D 2 2 = a 5 2 ⇒ V = 4 3 π R 3 = 5 π a 3 5 6

Đáp án A

Gọi O là giao điểm của 2 đường chéo AC và BIÊN ĐỘ, từ O dựng đường thẳng song song với SA và cắt SC tại trung điểm I của SC, suy ra I là tâm của mặt cầu ngoại tiếp hình chóp S.BCD
Mặt khác O I = 1 2 S A = a 2 O C = 1 2 A C = 1 2 a 2 + a 3 2 = a
Theo bài ra ta có: R = I C = O C 2 + O I 2 = a 5 2
Vậy thể tích khối cầu là V = 4 3 π a 5 2 3 = 5 π a 3 5 6

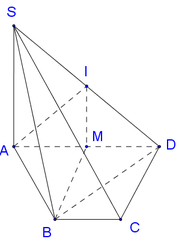

ABCD là hình thang cân có AB=CD=BC=2a,AD=2a ⇒ ABCD
là 1 nửa của hình lục giác đều, có tâm O là trung điểm của AD.
Gọi I là trung điểm của SD ⇒ OI//SA
Mà S A ⊥ ( A B C D ) ⇒ O I ⊥ ( A B C D ) ⇒ I là tâm mặt cầu ngoại tiếp
khối chóp S.ABCD ⇒ I là tâm mặt cầu ngoại tiếp khối chóp S.BCD.
Bán kính mặt cầu ngoại tiếp khối chóp S.BCD là:
R = S D 2 = S A 2 + A D 2 2 = 2 a 2 2 = a 2
Thể tích khối cầu đó là:
V = 4 3 πR 3 = 4 3 π a 2 3 = 8 πa 3 2 3
Chọn đáp án A.