Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
là trọng tâm tam giác SAE.
Tứ diện AEND vuông tại đỉnh A nên
Vậy
Do \(OC=\dfrac{1}{2}AC\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}d\left(A;\left(SCD\right)\right)\)
Kẻ \(AH\perp SD\Rightarrow AH\perp\left(SCD\right)\)
\(\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{SA.AD}{\sqrt{SA^2+AD^2}}=\sqrt{2}\)
\(\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}AH=\dfrac{\sqrt{2}}{2}\)
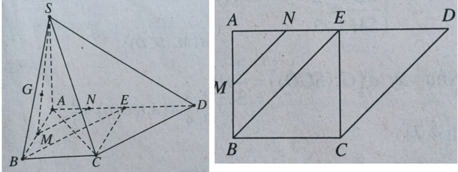
+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30 o .
∠(CSE) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
S E = C E . tan 60 o = a 3 ⇒ S A = S E 2 - A E 2 = 3 a 2 - a 2 = a 2 .
Nhận xét
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra
d(M,(SCD)) = d(N,(SCD)).
Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).
1: AC=căn a^2+a^2=a*căn 2
=>SC=căn SA^2+AC^2=a*căn 8
SB=căn AB^2+SA^2=a*căn 7
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
=>SB vuông góc BC
a: BC vuông góc SA
BC vuông góc AB
=>CB vuông góc (SBA)
DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SDC) vuông góc (SAD)
b: (SC;(SAD))=(SC;SD)=góc CSD
\(SD=\sqrt{SA^2+AD^2}=2a\sqrt{7}\)
\(AC=\sqrt{\left(2a\right)^2+3a^2}=a\sqrt{7}\)
\(SC=\sqrt{SA^2+AC^2}=4a\sqrt{2}\)
\(cosCSD=\dfrac{SC^2+SD^2-DC^2}{2\cdot SC\cdot SD}=\dfrac{32a^2+28a^2-4a^2}{2\cdot2a\sqrt{7}\cdot4a\sqrt{2}}=\dfrac{\sqrt{14}}{4}\)
=>góc CSD=21 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=5/căn 7
=>góc SCA=62 độ
Xét mặt phẳng đáy (ABCD) là hình thang cân. Kéo dài AC cắt BD tại I ta thu được tam giác đều ICD.
Do đó AD và BC đồng thời là đường cao và là đường trung tuyến của tam giác ICD. Suy ra O là trọng tâm của tam giác ICD (Với O là giao của AD và BC)
Ta có: \(AD=\sqrt{CD^2-AC^2}=a\sqrt{3}\)
\(\Rightarrow OA=\dfrac{1}{3}a\sqrt{3}\)
Vì hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) và có giao tuyến là SO. Do đó SO vuông góc với (ABCD)
Xét tam giác SOB vuông tại O ta có:
\(SO=\sqrt{SA^2-OA^2}=\dfrac{\sqrt{15}}{3}a\)
Vậy khoảng cách từ S đến mặt phẳng (ABCD) là \(\dfrac{\sqrt{15}}{3}a\)
Ta có: \(S_{ABCD}=\dfrac{3}{4}.S_{ICD}=\dfrac{3}{4}.\dfrac{AD.CI}{2}=\dfrac{3}{8}.a\sqrt{3}.2a=\dfrac{3\sqrt{3}}{4}a^2\)
\(\Rightarrow V_{S.ABCD}=\dfrac{1}{3}.SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{\sqrt{15}}{3}a.\dfrac{3\sqrt{3}}{4}a^2=\dfrac{\sqrt{5}}{4}a^3\)
Xét mặt phẳng đáy (ABCD) là hình thang cân. Kéo dài AC cắt BD tại I ta thu được tam giác đều ICD.
Do đó AD và BC đồng thời là đường cao và là đường trung tuyến của tam giác ICD. Suy ra O là trọng tâm của tam giác ICD (Với O là giao của AD và BC)
Ta có: \(AD=\sqrt{CD^2-AC^2}=a\sqrt{3}\)
\(\Rightarrow OA=\dfrac{1}{3}a\sqrt{3}\)
Vì hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) và có giao tuyến là SO. Do đó SO vuông góc với (ABCD)
Xét tam giác SOB vuông tại O ta có:
\(SO=\sqrt{SA^2-OA^2}=\dfrac{\sqrt{15}}{3}a\)
Vậy khoảng cách từ S đến mặt phẳng (ABCD) là \(\dfrac{\sqrt{15}}{3}a\)
Ta có: \(S_{ABCD}=\dfrac{3}{4}.S_{ICD}=\dfrac{3}{4}.\dfrac{AD.CI}{2}=\dfrac{3}{8}.a\sqrt{3}.2a=\dfrac{3\sqrt{3}}{4}a^2\)
\(\Rightarrow V_{S.ABCD}=\dfrac{1}{3}.SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{\sqrt{15}}{3}a.\dfrac{3\sqrt{3}}{4}a^2=\dfrac{\sqrt{5}}{4}a^3\)
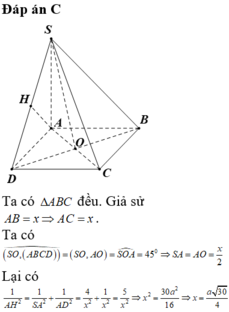
d(B;(SCD))=1/2*d(A;(SCD))
Gọi giao của AB và CD là E
BC//AD
=>EB/EA=EC/ED=BC/AD=1/2
=>ΔAED cân tại E
=>AC vuông góc DE
Kẻ AF vuông góc SC
\(AC=\sqrt{2^2-1^2}=\sqrt{3}\left(cm\right)\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{6}\left(cm\right)\)
=>\(AF=d\left(A;\left(SCD\right)\right)=\dfrac{3}{\sqrt{6}}=\dfrac{\sqrt{6}}{2}\left(cm\right)\)
=>\(d\left(B;\left(SCD\right)\right)=\dfrac{\sqrt{6}}{4}\left(cm\right)\)