K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

Q
1 tháng 4 2017
a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:

QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
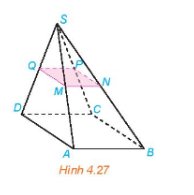
Xét tam giác SAB ta có: MN là đường trung bình suy ra MN // AB.
Tương tự ta có: NP // BC, PQ // CD, MQ // AD.
Mà ABCD là hình bình hành nên AB // CD, AD// CD, suy ra MN // PQ, MQ // NP.
Như vậy, MNPQ là hình bình hành.





Đáp án B