Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
=>(SAD) vuông góc (SCD)
b: (SCD) giao (ABCD)=CD
CD vuông góc (SAD)
=>CD vuông góc SD
CD vuông góc SD
AD vuông góc CD
mà SD thuộc (SCD) và AD thuộc (ABCD)
nên ((SCD);(ABCD))=(SD;AD)=góc SDA
tan SDA=SA/AD=căn 3/2
=>góc SDA=41 độ

S A B C D K
gọi K thuộc SC sao cho DK \(\perp\) SC , BK \(\perp\)SC
=> ((SCD),(SBC)) = (DK,KB)
tính được SD = \(\frac{\sqrt{10}}{2}\)a, AC = \(\sqrt{3}\)a, SC= \(\frac{3\sqrt{2}}{2}\)a
\(DC^2=SD^2+SC^2-2SD.SC.cos\widehat{DSC}\)
=> \(\widehat{DSC}\)=....... (số xấu)
\(sin\widehat{DSC}\)= \(\frac{DK}{SD}\)=> DK = \(\frac{\sqrt{2}}{2}\)=BK
\(DB^2=DK^2+BK^2-2.DK.BK.cos\alpha\)=> \(\alpha=\frac{\pi}{2}\)

Gặp những bài cần tính toán thế này làm biếng lắm, dựng hình thì dễ chứ tính thì chả muốn tính chút xíu nào.
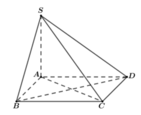
Trong mp đáy, kéo dài AD và BC cắt nhau tại E \(\Rightarrow D\) là trung điểm AE (đường trung bình) \(\Rightarrow AE=AB=2a\)
Ta có: \(\left\{{}\begin{matrix}AD\perp AB\\SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\Rightarrow AD\perp SB\)
\(\Rightarrow AD\in\left(\alpha\right)\)
Trong mp (SAB), kẻ \(AM\perp SB\Rightarrow M\in\left(\alpha\right)\)
Dễ dàng chứng minh tam giác ACB vuông cân tại C (Pitago đảo) \(\Rightarrow BC\perp\left(SAC\right)\)
Trong mp (SAC), kẻ \(AN\perp SC\Rightarrow AN\perp\left(SBC\right)\Rightarrow AN\perp SB\Rightarrow N\in\left(\alpha\right)\)
\(\Rightarrow\) Thiết diện là tứ giác AMND
\(SB=SE=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(AM=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{2a\sqrt{5}}{5}\)
\(AC=a\sqrt{2}\Rightarrow SC=\sqrt{AC^2+SA^2}=a\sqrt{3}\)
\(CN=\dfrac{AC^2}{SC}=\dfrac{2a\sqrt{3}}{3}\) ; \(EC=BC=a\sqrt{2}\Rightarrow EN=\sqrt{EC^2+CN^2}=\dfrac{a\sqrt{30}}{3}\)
\(DE=AD=a\)
\(S_{AME}=\dfrac{1}{2}AM.AE=...\)
\(S_{DNE}=\dfrac{1}{2}DE.EN.sin\widehat{DEN}=\dfrac{1}{2}DE.EN.\dfrac{AM}{\sqrt{AM^2+AE^2}}=...\)
\(\Rightarrow S_{AMND}=S_{AME}-S_{DNE}=...\)

Chọn C, bởi vì AC ko thể vuông góc với SB và SD được mà chỉ có thể vuông góc với BD thôi

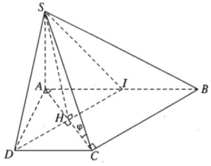
a) Ta có:
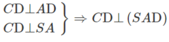
⇒ (SCD) ⊥ (SAD)
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
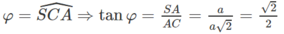
c) 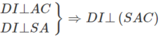
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và 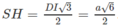 .
.
Tam giác SDI có diện tích:
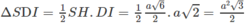

Chọn B
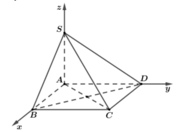
Để cho gọn ta chọn a =1
Chọn hệ trục tọa độ sao cho A = O(0;0;0) và B(1;0;0), D(0;1;0) S(0;0;x) với x = SA >0
Suy ra C(1;1;0)
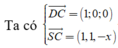
=> VTPT của mặt phẳng (SCD) là
![]()
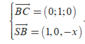
=> VTPT của mặt phẳng (SBC) là
![]()
Từ giả thiết bài toán, ta có
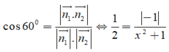
![]()

S A B C D H O M N P Q K E I
a/
Ta có
\(CB\perp AB\) (ABCD là hình vuông)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CB\)
\(\Rightarrow CB\perp\left(SAB\right)\) => CB=a là khoảng cách từ C đến mp (SAB)
b/
Trong mp (SAD) dựng đường thẳng vuông góc với SD cắt SD tại H
Ta có
\(CD\perp AD\) (ABCD là hình vuông)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\)
\(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AH\)
Mà \(AH\perp SD\)
\(\Rightarrow AH\perp\left(SCD\right)\) => AH là khoảng cách từ A đến mp (SCD)
Xét tg vuông SAD có
\(SD=\sqrt{SA^2+AD^2}=\sqrt{2a^2+a^2}=a\sqrt{3}\) (Pitago)
Ta có
\(AD^2=DH.SD\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow DH=\dfrac{AD^2}{SD}=\dfrac{a^2}{a\sqrt{3}}=\dfrac{a\sqrt{3}}{3}\)
Xét tg vuông ADH có
\(AH=\sqrt{AD^2-DH^2}\) (Pitago)
\(\Rightarrow AH=\sqrt{a^2-\dfrac{a^2}{3}}=\dfrac{a\sqrt{6}}{3}\)
c/ Trong mp (ABCD) Qua O dựng đường thẳng //CD cắt AD tại M và BC tại N => MN//CD (1)
Trong mp (SAD) dựng đường thẳng // AH cắt SD tại Q => MQ // AH
TRong mp (SCD) qua Q dựng đường thẳng //CD cắt SC tại P => QP // CD (2)
Từ (1) và (2) => MN // PQ => M; N; P; Q cùng thuộc 1 mặt phẳng
=> PQ là giao tuyến của mp (MNQP) với mp (SCD)
Trong mp (MNQP) qua O dựng đường thẳng // với MQ cắt QP tại K
Ta có
MQ//AH; OH// MQ => OK//AH
Mà \(AH\perp\left(SCD\right)\)
\(\Rightarrow OK\perp\left(SCD\right)\) => OK là khoảng cách từ O đến mp (SCD)
Xét tứ giác MQKO có
MQ//OK; QP//MN => MQKO là hình bình hành => OK = MQ
Xét tg ACD có
OA=OC (t/c đường chéo hình vuông)
MO//CD
=> MA=MD (trong tg đường thẳng đi qua trung điểm của 1 cạnh // với cạnh thứ 2 thì đi qua trung điểm cạnh còn lai)
Xét tg ADH có
MA=MD (cmt); MQ//AH => QD = QH (trong tg đường thẳng đi qua trung điểm của 1 cạnh // với cạnh thứ 2 thì đi qua trung điểm cạnh còn lai)
=> MQ là đường trung bình của tg ADH
\(\Rightarrow OK=MQ=\dfrac{AH}{2}=\dfrac{1}{2}.\dfrac{a\sqrt{6}}{3}=\dfrac{a\sqrt{6}}{6}\)
d/
Trong mp (SCD) qua H dựng đường thẳng //CD cắt SC tại E => HE//CD
Ta có
AB // CD (Hai cạnh đối hình vuông)
HE // CD
=> AB//HE => A; B; H; E cùng thuộc một mặt phẳng
Trong mp (AHEB) qua e Dựng đường thẳng // AH cắt AB tại I
Ta có
AH//IE; AB//HE => AHEB là hình bình hành => IE=AH
Ta có
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\)
\(AB\perp AD\) (ABCD là hình vuông)
=> \(AB\perp\left(SAD\right)\Rightarrow AB\perp AH\)
Mà AH//IE
\(\Rightarrow AB\perp IE\) (1)
Ta có
\(AH\perp\left(SCD\right)\) (cmt); mà AH//IE \(\Rightarrow IE\perp\left(SCD\right)\Rightarrow IE\perp SC\) (2)
Từ (1) và (2) => IE là khoảng cách giữa AB và SC
\(\Rightarrow IE=AH=\dfrac{a\sqrt{6}}{3}\)

Chọn D.
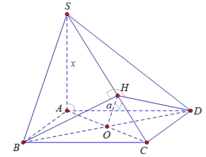
- Kẻ BH ⊥ SC ⇒ DH ⊥ SC (hai đường cao tương ứng của hai tam giác bằng nhau).
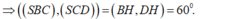
- Có 2 trường hợp xảy ra:
TH1:
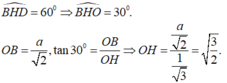
- Xét hai tam giác đồng dạng SAC và OHC ta có

TH2:
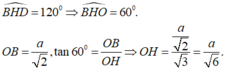
- Xét hai tam giác đồng dạng SAC và OHC ta có:
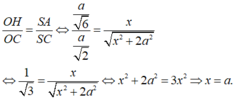

Đáp án B.
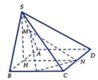
Gọi H là trung điểm của cạnh AB. Khi đó SH ⊥ (ABCD)
Ta có SH ⊥ AB; AB ⊥ HN; HN ⊥ SH và SH = 3
Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó: B(1;0;0), A(-1;0;0), N(0;2 3 ;0), C(1;2 3 ;0)
D(-1;2 3 ;0), S(0;0; 3 ), M( - 1 2 ; 0 ; 3 2 ), P(1; 3 ;0)
Mặt phẳng (SCD) nhận
![]()
làm một vectơ pháp tuyến; mặt phẳng (MNP) nhận
![]()
làm một vectơ pháp tuyến.
Gọi φ là góc tạo bởi hai mặt phẳng (MNP) và (SCD) thì
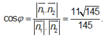
Phân tích phương án nhiễu.
Phương án A: Sai do HS tính đúng
![]()
nhưng lại tính sai ![]() Do đó tính được
Do đó tính được
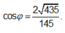
Phương án B: Sai do HS tính đúng ![]() nhưng lại tính sai
nhưng lại tính sai
![]()
Do đó tính được
![]()
Phương án C: Sai do HS tính đúng ![]() nhưng lại tính sai
nhưng lại tính sai
![]() Do đó tính được
Do đó tính được 
Chọn D