Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
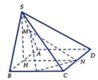
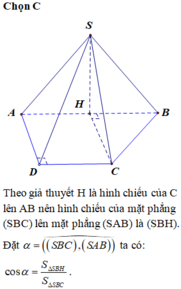
Gọi H là trung điểm của cạnh AB. Khi đó SH ⊥ (ABCD)
Ta có SH ⊥ AB; AB ⊥ HN; HN ⊥ SH và SH = 3
Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó: B(1;0;0), A(-1;0;0), N(0;2 3 ;0), C(1;2 3 ;0)
D(-1;2 3 ;0), S(0;0; 3 ), M( - 1 2 ; 0 ; 3 2 ), P(1; 3 ;0)
Mặt phẳng (SCD) nhận
![]()
làm một vectơ pháp tuyến; mặt phẳng (MNP) nhận
![]()
làm một vectơ pháp tuyến.
Gọi φ là góc tạo bởi hai mặt phẳng (MNP) và (SCD) thì
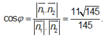
Phân tích phương án nhiễu.
Phương án A: Sai do HS tính đúng
![]()
nhưng lại tính sai ![]() Do đó tính được
Do đó tính được
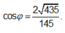
Phương án B: Sai do HS tính đúng ![]() nhưng lại tính sai
nhưng lại tính sai
![]()
Do đó tính được
![]()
Phương án C: Sai do HS tính đúng ![]() nhưng lại tính sai
nhưng lại tính sai
![]() Do đó tính được
Do đó tính được 

Chọn A

Gọi H là trung điểm AB
![]()
nên hình chiếu của SD trên (ABCD) là HD
![]()
Tam giác SAB đều cạnh a nên SH = a 3 2
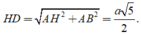
Tam giác vuông SHD
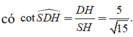

Chọn đáp án A
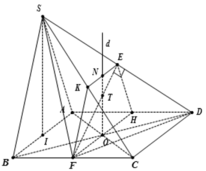
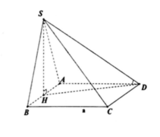
+ Gọi O là tâm của hình vuông ABCD. Qua O ta dựng đường thẳng d vuông góc với mặt đáy.
+ Gọi E, K, F, H, N lần lượt là trung điểm của các đoạn thẳng SD, SC, BC, AD, EK
+ Ta có tam giác SDF là tam giác cân tại F. Vì FD = FS = a 5 (độc giả tự chứng minh)
Suy ra FE ⊥ SD
Mặt khác, ta có KE // FH (Vì cùng song song với CD). Nên 4 điểm K, E, F, H đồng phẳng
+ Trong mặt phẳng (KEFH), gọi T là giao điểm của FE và ON.
Ta có T là tâm mặt cầu ngoại tiếp hình chóp S. ABCD
+ Ta có tam giác EKO là tam giác đều cạnh a. Nên
![]()
Bán kính mặt cầu là
![]()
+ Xét tam giác vuông TOB vuông tại B, ta có
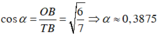
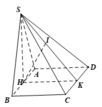
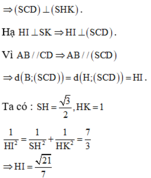


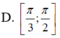
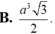
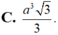
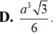
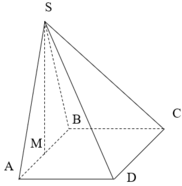
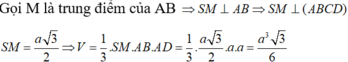
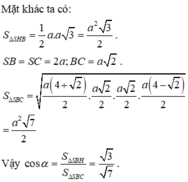
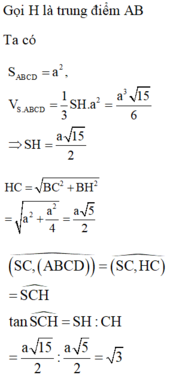
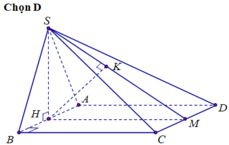

Lời giải:
Gọi $H$ là trung điểm của $AB$. Vì $SAB$ là tam giác đều nên $SH\perp AB$. Mà $AB=(SAB)\cap (ABCD)$ và $(SAB)\perp (ABCD)$
$\Rightarrow SH\perp (ABCD)$
Gọi $M$ là trung điểm $CD$ thì $HM\perp CD$. Mà $SH\perp CD$ (do $SH\perp (ABCD))$
$\Rightarrow (SHM)\perp CD$
$CD$ là giao tuyến của $(SCD), (ABCD)$
$\Rightarrow \angle ((SCD), (ABCD))=\angle (SM, HM)=\widehat{SMH}$
Tam giác $SHM$ vuông tại $H$ có:
$SH=\frac{\sqrt{3}}{2}AB = \frac{\sqrt{3}}{2}a$
$HM=AD=a$
$\Rightarrow \tan \widehat{SMH}=\frac{SH}{HM}=\frac{\sqrt{3}}{2}$
$\Rightarrow \angle ((SCD), (ABCD))=\widehat{SMH}\approx 41^0$