Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC vuông góc SA
BC vuông góc AB
=>CB vuông góc (SBA)
DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SDC) vuông góc (SAD)
b: (SC;(SAD))=(SC;SD)=góc CSD
\(SD=\sqrt{SA^2+AD^2}=2a\sqrt{7}\)
\(AC=\sqrt{\left(2a\right)^2+3a^2}=a\sqrt{7}\)
\(SC=\sqrt{SA^2+AC^2}=4a\sqrt{2}\)
\(cosCSD=\dfrac{SC^2+SD^2-DC^2}{2\cdot SC\cdot SD}=\dfrac{32a^2+28a^2-4a^2}{2\cdot2a\sqrt{7}\cdot4a\sqrt{2}}=\dfrac{\sqrt{14}}{4}\)
=>góc CSD=21 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=5/căn 7
=>góc SCA=62 độ

Tuy nhiên đề cho giá trị cạnh AC với BC bị sai. Cạnh huyền AC (\(a\sqrt{3}\)) sao lại có giá trị nhỏ hơn cạnh góc vuông BC (2a) nhỉ?

a. Do \(\left\{{}\begin{matrix}SA=\left(SAB\right)\cap\left(SAD\right)\\\left(SAB\right)\perp\left(ABCD\right)\\\left(SAD\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
b.
\(SA\perp\left(ABCD\right)\Rightarrow AD\) là hình chiếu vuông góc của SD lên (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa SD và (ABCD) \(\Rightarrow\widehat{SDA}=60^0\)
\(tan\widehat{SDA}=\dfrac{SA}{AD}\Rightarrow SA=AD.tan\widehat{SDA}=2a\sqrt{3}\)
c.
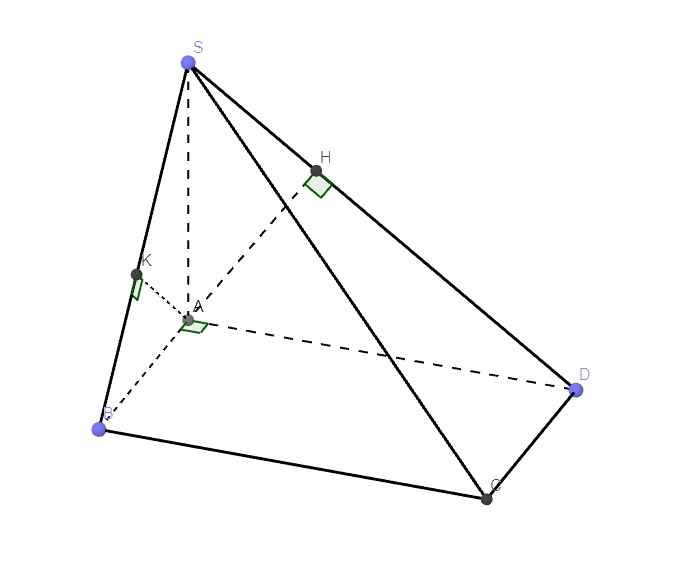
Từ A kẻ \(AH\perp SD\) (1)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AH\) (2)
(1);(2) \(\Rightarrow AH\perp\left(SCD\right)\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
\(AH=AD.sin\widehat{SDA}=2a.sin60^0=a\sqrt{3}\)
d.
Ta có: \(AI||BC\Rightarrow d\left(I;\left(SBC\right)\right)=d\left(A;\left(SBC\right)\right)\)
Trong tam giác vuông SAB, kẻ \(AK\perp SB\)
Tương tự câu c, dễ dàng chứng minh \(AK\perp\left(SBC\right)\Rightarrow AK=d\left(A;\left(SBC\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{AK^2}=\dfrac{1}{AB^2}+\dfrac{1}{SA^2}=\dfrac{13}{12a^2}\Rightarrow AK=\dfrac{2a\sqrt{39}}{13}\)

a: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
b: (SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=1/2
=>góc SDA=27 độ



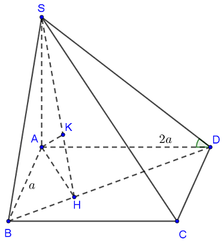
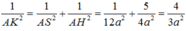
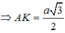

Theo đề có:
\(\left\{{}\begin{matrix}CD\perp AD\\CD\perp SA\end{matrix}\right.\)
=> \(CD\perp\left(SAD\right)\)
<=> \(d\left(C,\left(SAD\right)\right)=CD=a\)
`HaNa♬`