Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

.png)
+ SA⊥(ABCD)⇒SA⊥BDSA⊥(ABCD)⇒SA⊥BD (1)
+ ABCD là hình vuông ⇒AC⊥BD⇒AC⊥BD (2)
+ Từ (1) và (2) suy ra BD⊥(SAC)⇒BD⊥SCBD⊥(SAC)⇒BD⊥SC

\(\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)\)
Kẻ \(IH \bot BC\left( {H \in BC} \right)\)
\(SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC\)
\( \Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {AHI}\) là góc nhị diện \(\left[ {S,BC,A} \right]\)\( \Rightarrow \widehat {AHI} = {60^ \circ }\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} - {S_{AIB}} - {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}\)
Gọi \(M\) là trung điểm của \(AB\)
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}} = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}\)

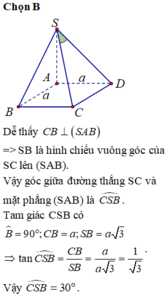
\(\left\{{}\begin{matrix}BD\perp AC\left(\text{ABCD là hình vuông}\right)\\SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AC\)
\(\Rightarrow BD\in\left(\alpha\right)\)
Trong mp (SBC), từ B kẻ \(BE\perp SC\Rightarrow E\in\left(\alpha\right)\)
\(\Rightarrow\) Tam giác BDE là thiết diện của chóp và \(\left(\alpha\right)\)
\(BD=AB\sqrt{2}=a\sqrt{2}\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) hay tam giác SBC vuông tại B
\(SB=\sqrt{SA^2+AB^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{BE^2}=\dfrac{1}{SB^2}+\dfrac{1}{BC^2}-\dfrac{1}{4a^2}+\dfrac{1}{a^2}=\dfrac{5}{4a^2}\Rightarrow BE=DE=\dfrac{2a\sqrt{5}}{5}\)
\(\Rightarrow OE=\sqrt{BE^2-\left(\dfrac{BD}{2}\right)^2}=\dfrac{a\sqrt{30}}{10}\)
\(S_{BDE}=\dfrac{1}{2}OE.BD=\dfrac{a^2\sqrt{15}}{10}\)

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=45^0\Rightarrow AC=SA=a\sqrt{2}\)
\(\Rightarrow AB=a\)
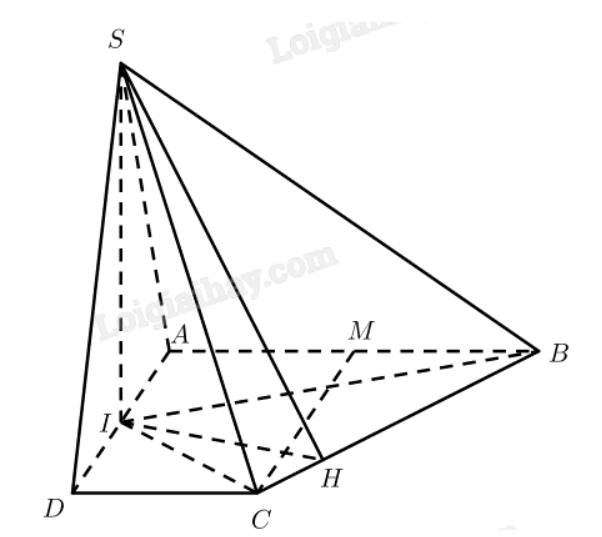
Gọi N là trung điểm SA \(\Rightarrow NM||SB\Rightarrow SB||\left(DMN\right)\)
\(\Rightarrow d\left(DM;SB\right)=d\left(SB;\left(DMN\right)\right)=d\left(B;\left(DMN\right)\right)\)
Mà M là trung điểm AB \(\Rightarrow d\left(B;\left(DMN\right)\right)=d\left(A;\left(DMN\right)\right)\)
Từ A kẻ AH vuông góc DM \(\Rightarrow DM\perp\left(NAH\right)\)
Trong mp (NAH), từ A kẻ \(AK\perp NH\Rightarrow AK=d\left(A;\left(DMN\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AM.AD}{\sqrt{AM^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AN^2}+\dfrac{1}{AH^2}\Rightarrow AK=\dfrac{AN.AH}{\sqrt{AN^2+AH^2}}=\dfrac{a\sqrt{7}}{7}\)

a.
Do AB song song DC nên góc giữa SC và AB là góc giữa SC và CD, cùng là góc SCD
Áp dụng định lý hàm cosin:
\(cos\widehat{SCD}=\dfrac{SC^2+CD^2-SD^2}{2SC.CD}=\dfrac{1}{4}\)
\(\Rightarrow\widehat{SCD}\approx75^031'\)
b.
Gọi O là tâm đáy, do chóp có đáy là hình vuông và các cạnh bên bằng nhau nên chóp là chóp đều
\(\Rightarrow SO\perp\left(ABCD\right)\)
\(\Rightarrow\Delta OAB\) là hình chiếu vuông góc của SAB lên (ABCD)
\(OA=OB=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AB^2+BC^2}=a\)
Mặt khác OA vuông góc OB (2 đường chéo hình vuông)
\(\Rightarrow S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{a^2}{2}\)

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow\widehat{BSC}\) là góc giữa SC và (SAB)
\(tan\widehat{BSC}=\dfrac{BC}{SB}=\dfrac{\sqrt{10}}{5}\Rightarrow SB=\dfrac{a\sqrt{10}}{2}\)
\(\Rightarrow SA=\sqrt{SB^2-AB^2}=\dfrac{a\sqrt{6}}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(AO=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{3}\Rightarrow\widehat{SOA}=60^0\)

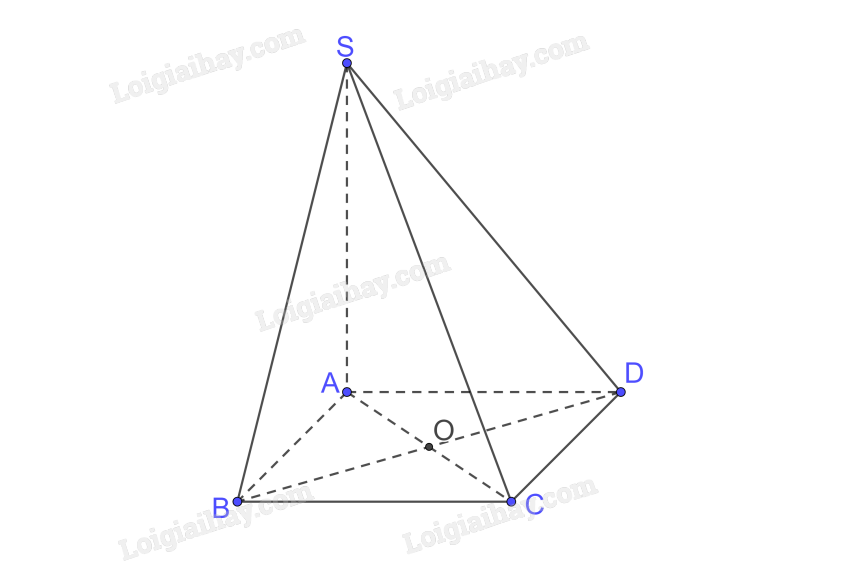
a) A là hình chiếu của S trên (ABCD) \(\left( {SA \bot \left( {ABCD} \right)} \right)\)
C là hình chiếu của C trên (ABCD)
\( \Rightarrow \) AC là hình chiếu của SC trên (ABCD)
\( \Rightarrow \) \(\left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Xét tam giác SAC vuông tại A có
\(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{a\sqrt 2 }}{{a\sqrt 2 }} = 1 \Rightarrow \widehat {SCA} = {45^0}\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {45^0}\)
b) \(\left. \begin{array}{l}AC \bot BD\left( {hv\,\,ABCD} \right)\\SA \bot BD\left( {SA \bot \left( {ABCD} \right)} \right)\\AC \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow \left( {BD,\left( {SAC} \right)} \right) = {90^0}\)
c) Gọi \(AC \cap BD = \left\{ O \right\}\) mà \(BD \bot \left( {SAC} \right)\)
\( \Rightarrow \) O là hình chiếu của B trên (SAC)
S là hình chiếu của S trên (SAC)
\( \Rightarrow \) SO là hình chiếu của SB trên (SAC).