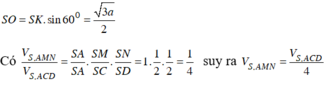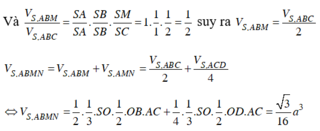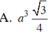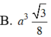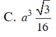Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

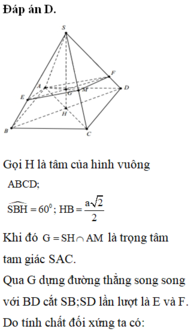
Qua G kẻ đường thẳng d song song với AB.
\(H=d\cap SB;K=d\cap SA\)
Kẻ KP//AD, HT//BC \(\left(P\in SD;T\in SC\right)\)
\(\Rightarrow KHTP\) là thiết diện cần tìm.
\(\dfrac{HK}{AB}=\dfrac{HT}{BC}=\dfrac{KP}{AD}=\dfrac{PT}{CD}=\dfrac{2}{3}\)
Mà \(AB=BC=CD=DA\Rightarrow KH=HT=TP=PK\)
\(\Rightarrow KHPT\) là hình vuông.

Chọn đáp án C
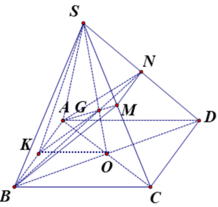
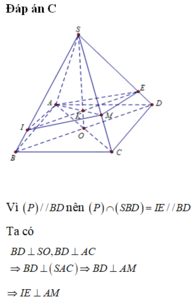
Do S. ABCD đều, có trọng tâm G của tam giác SAC cũng là trọng tâm của SBD.
Nên M, N lần lượt là trung điểm của SC, SD.
Do đó
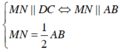
Gọi K là trung điểm của AB, O = AC ∩ BD do S. ABCD đều nên SO ⊥ (ABCD)
ABCD là hình vuông nên có SKO = 60 0
Xét tam giác SKO vuông tại O có KO = a 2 và SKO = 60 0 suy ra: