
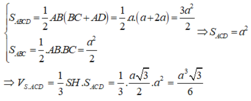
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


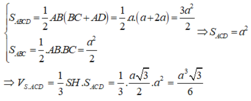

S o B H A D G d H' C K
Câu a bạn tự tính nhé!
Câu b: Qua G kẻ đường thẳng d // CD , khoảng cách từ \(d\left(G;\left(SAB\right)\right)=d\left(d;\left(SAD\right)\right)\)
Kẻ HH' vuông CD , nối SH'. Lúc này SH' cách d tại K . \(d\left(K;\left(SAB\right)\right)\) là khoảng cách cần tìm.
Ta có: SH'AB =\(\frac{1}{2}S_{ABCD}\)=\(\frac{1}{2}\times2\sqrt{3}a^2=\sqrt{3}a^2\) \(\Rightarrow HH'=\frac{\sqrt{3}a^2}{a}=\sqrt{3}a\)
Vì K nằm trên d nên \(d\left(K;\left(SAB\right)\right)=\frac{2}{3}HH'=\frac{2\sqrt{3}a}{3}\)

1, Đổi chỗ 3 viên ở 3 đỉnh tam giác: viên dưới cùng lên đỉnh trên cùng, 2 viên ngoài cùng ở 2 bên đảo xuốn đáy
2, 8-6+2=4; 12-5+8=15; 13-10+15=18. x=15
3,
*) \(5^3+5=130;3^3+3=30;2^3+2=10;1^3+1=2\)
*) 2+3=8 hay 2.(2+3)-2=8
4+5=32 hay 4.(4+5)-4=32
5+8=60 hay 5.(5+8)-5=60
6+7=72 hay 6.(6+7)-6=72
7+8= 7.(7+8)-7=98

S H B K A I C D
Gọi K là hình chiếu của I lên AB
Suy ra \(\widehat{SKI=60^0}\)
Mà \(\frac{BI}{ID}=\frac{BC}{AD}=\frac{a}{3a}=\frac{1}{2}\)\(\Rightarrow\frac{BI}{BI+ID}=\frac{1}{4}\)\(\Rightarrow\frac{BI}{BD}=\frac{1}{4}\)
Suy ra \(\frac{KI}{DA}=\frac{1}{4}\)\(\Rightarrow KI=\frac{3a}{4}\Rightarrow SI=\frac{3a\sqrt{3}}{4}\)
Do \(IK\) \\ \(AD\Rightarrow\frac{KI}{AD}=\frac{BI}{BD}\)
\(V_{A.ABCD}=\frac{1}{3}.SI.S_{ABCD}=\frac{1}{3}.\frac{3a\sqrt{3}}{4}.\frac{1}{2}\left(a+3a\right)a=\frac{a^3\sqrt{3}}{2}\)
Gọi H là hình chiếu của I trên SK. Ta có \(\begin{cases}AB\perp IK\\AB\perp SI\end{cases}\)\(\Rightarrow AB\perp IH\)
Từ đó suy ra \(IK\perp\left(SAB\right)\Rightarrow d\left(I,\left(SAB\right)\right)=IK\)
Mà do \(DB=4IB\Rightarrow\left(D,\left(SAB\right)\right)=4d\left(I,\left(SAB\right)\right)=4IH\)
Lại có \(\frac{1}{IH^2}=\frac{1}{IS^2}+\frac{1}{IK^2}=\frac{16}{27a^2}+\frac{16}{9a^2}=\frac{64}{27a^2}\Leftrightarrow IH=\frac{3a\sqrt{3}}{8}\)
Vậy \(d\left(D,\left(SAB\right)\right)=\frac{3a\sqrt{3}}{2}\)

Đáp án A
Ta có tam giác ACD vuông cân tại C và C A = C D = 2 a 2
⇒ S ∆ A C D = 4 a 2 . Gọi H là trung điểm của AB
Vì tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy
⇒ S H ⊥ ( A B C D ) ; S H = a 3 .
Vậy S S . A C D = 4 a 3 3 3 .

Em chỉ cần chú ý là bán \(\dfrac{1}{2}\) số còn lại mà đang còn dư 18 lít thì số còn lại sau khi bán một nửa là 36 lít. Từ đó suy ra cả thùng chưa bán có tất cả 72 lít