Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
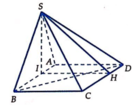
Ta có AD//BC, ![]() => AD//(SBC)
=> AD//(SBC)
=> d(AD;SC) = d(AD;(SBC)) = d(D;(SBC)).
Qua I kẻ đường thẳng song song với AD, cắt CD tại H.
Suy ra IH ⊥ CD
Từ CD ⊥ IH, CD ⊥ SI=> CD ⊥ (SIH)=> CD ⊥ SH
Suy ra ![]()
![]()
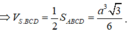
Lại có
![]()
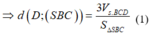
Từ ![]()
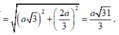
![]()
![]()
Suy ra
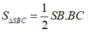
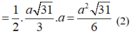
Từ (1) và (2), suy ra
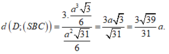
Vậy
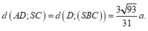

Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
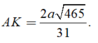

Đáp án B
Ta có d(K;(SCD)) 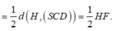
Ta có
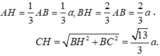
Có góc giữa SC và đáy là nên ta có
![]()

Ta có 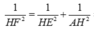
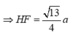

\(\left\{{}\begin{matrix}\left(SAB\right)\cap\left(SAD\right)=SA\\\left(SAB\right)\perp\left(ABCD\right)\\\left(SAD\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
Gọi N là trung điểm BC \(\Rightarrow MN||AB\Rightarrow AB||\left(SMN\right)\)
\(\Rightarrow d\left(AB;SM\right)=d\left(AB;\left(SMN\right)\right)=d\left(A;\left(SMN\right)\right)\)
Từ A kẻ \(AH\perp SM\)
\(\left\{{}\begin{matrix}MN||AB\Rightarrow MN\perp AD\\SA\perp\left(ABCD\right)\Rightarrow SA\perp MN\end{matrix}\right.\) \(\Rightarrow MN\perp\left(SAD\right)\Rightarrow MN\perp AH\)
\(\Rightarrow AH\perp\left(SMN\right)\Rightarrow AH=d\left(A;\left(SMN\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow SA=\sqrt{SC^2-AC^2}=a\)
\(AM=\dfrac{AD}{2}=\dfrac{a}{2}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AM^2}\Rightarrow AH=\dfrac{SA.AM}{\sqrt{SA^2+AM^2}}=\dfrac{a\sqrt{5}}{5}\)

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=45^0\Rightarrow AC=SA=a\sqrt{2}\)
\(\Rightarrow AB=a\)
Gọi N là trung điểm SA \(\Rightarrow NM||SB\Rightarrow SB||\left(DMN\right)\)
\(\Rightarrow d\left(DM;SB\right)=d\left(SB;\left(DMN\right)\right)=d\left(B;\left(DMN\right)\right)\)
Mà M là trung điểm AB \(\Rightarrow d\left(B;\left(DMN\right)\right)=d\left(A;\left(DMN\right)\right)\)
Từ A kẻ AH vuông góc DM \(\Rightarrow DM\perp\left(NAH\right)\)
Trong mp (NAH), từ A kẻ \(AK\perp NH\Rightarrow AK=d\left(A;\left(DMN\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AM.AD}{\sqrt{AM^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AN^2}+\dfrac{1}{AH^2}\Rightarrow AK=\dfrac{AN.AH}{\sqrt{AN^2+AH^2}}=\dfrac{a\sqrt{7}}{7}\)

SA vuông gớc (ABCD)
=>(SM;(ABCD))=góc SMA
=>cos(SM;(ABCD))=cos SMA=AM/SM
(SC;(ABCD))=góc SCA
=>góc SCA=45 độ
=>ΔSAC vuông cân tại A
=>AS=AC=căn AB^2+BC^2=4a
=>SM^2=SA^2+AM^2=29a^2
=>SM=a*căn 29
=>cos(SM;(ABCD))=AM/SM=căn 377/29

Gọi N là trung điểm AB \(\Rightarrow MN\perp AD\Rightarrow AD\perp\left(SMN\right)\Rightarrow AD\perp SM\)
Mặt khác: \(MN=AB=a\) ; \(SM=SN=\sqrt{SO^2+\left(\dfrac{MN}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow SM^2+SN^2=MN^2\Rightarrow\Delta SMN\) vuông cân tại S hay \(SM\perp SN\)
\(\Rightarrow SM\perp\left(SAD\right)\)
Trong mp (SBC), dựng hình chữ nhật SMCP \(\Rightarrow CP||SM\Rightarrow CP\perp\left(SAD\right)\)
\(\Rightarrow\) SP là hình chiếu vuông góc của SC lên (SAD) hay \(\widehat{CSP}=\phi\)
\(AC=a\sqrt{5}\Rightarrow SC=\sqrt{SO^2+\left(\dfrac{AC}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\); \(SP=MC=\dfrac{BC}{2}=a\)
\(\Rightarrow CP=\sqrt{SC^2-SP^2}=\dfrac{a\sqrt{2}}{2}\)
\(sin\phi=\dfrac{CP}{SC}=\dfrac{\sqrt{3}}{3}\)
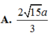
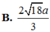
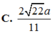


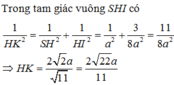
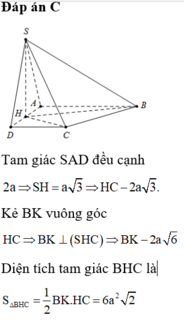
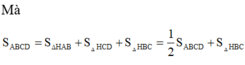
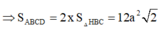
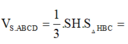
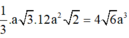

Hệ thức lượng: \(SA^2=AH.AD=\dfrac{3}{4}AD^2\)
\(\Rightarrow AD=4a\) \(\Rightarrow AH=3a\) ; \(HD=a\)
\(\Rightarrow SH=\sqrt{SA^2-AH^2}=a\sqrt{3}\)
\(HC=\dfrac{SH}{tan30^0}=3a\) \(\Rightarrow CD=\sqrt[]{HC^2-HD^2}=2a\sqrt{2}\)
\(\Rightarrow AM=\dfrac{1}{2}AB=\dfrac{1}{2}CD=a\sqrt{2}\)
Qua M kẻ đường thẳng song song BD cắt AD tại F.
Từ H kẻ \(HE\perp MF\), từ H kẻ \(HK\perp SF\)
\(\Rightarrow HK=d\left(H;\left(SME\right)\right)\)
MF là đường trung bình tam giác ABD \(\Rightarrow AD=FD=\dfrac{1}{2}AD=2a\Rightarrow HF=a\)
\(HE=HF.sin\widehat{EFH}=HF.sin\widehat{AFM}=HF.\dfrac{AM}{\sqrt{AM^2+AF^2}}=\)
\(\Rightarrow HK=\dfrac{HE.SH}{\sqrt{HE^2+SH^2}}=\)
\(DE=2HE\Rightarrow d\left(SM;BD\right)=d\left(D;\left(SME\right)\right)=2HK=\)