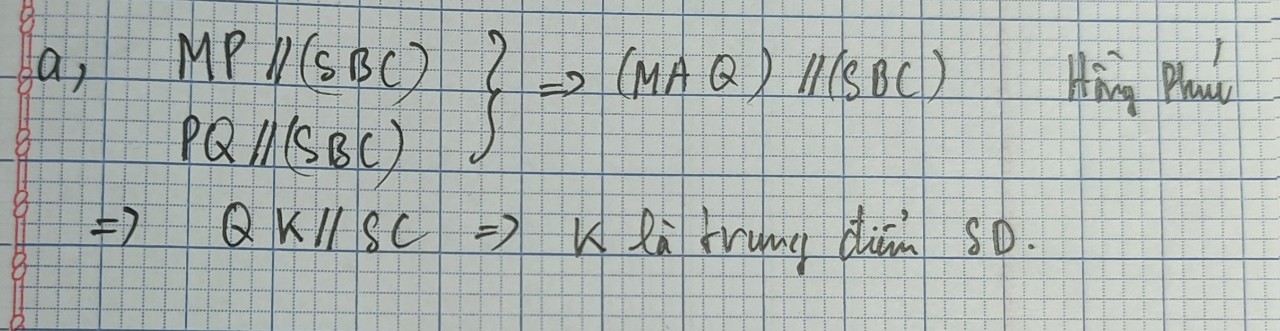Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có AB//CD \(\Rightarrow\) AB//(MNPQ)
SB//MN \(\Rightarrow\) SB//(MNPQ)
\(\Rightarrow\) (SAB)//(MNPQ)
Mà \(\left\{{}\begin{matrix}SA=\left(SAD\right)\cap\left(SAB\right)\\PQ=\left(SAD\right)\cap\left(MNPQ\right)\end{matrix}\right.\) \(\Rightarrow\) SA//PQ
b/ Ta có \(K\in\left(SAD\right);K\in\left(SBC\right)\Rightarrow SK=\left(SAD\right)\cap\left(SBC\right)\)
\(\Rightarrow K\) thuộc giao tuyến (SAD) và (SBC)
Mà giao tuyến (SAD) và (SBC) là đường thẳng cố định qua S song song AD và BC \(\Rightarrow\) K thuộc 1 đường thẳng cố định

Đáp án B
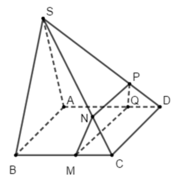
Ta có: MN // BS ⇒ C M C B = C N C S
MQ // CD // AB (do ABCD là hình bình hành nên AB //CD) ⇒ C M C B = D Q D A
NP // CD ⇒ C N C S = D P D S
Do đó: D P D S = D Q D A PQ // SA (Định lý Ta - lét trong tam giác SAD)
Lại có MN // BS và SB ∩ SA = S
Do đó MN không thể song song với PQ
Xét tứ giác MNPQ có NP // MQ (//CD)
Do đó MNPQ là hình thang.
Vậy khẳng địn (1) và (3) đúng.
Đáp án B

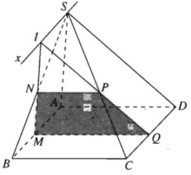
a) Vì M ∈ (SAB)
Và 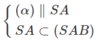 nên (α) ∩ (SAB) = MN
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và 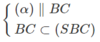 nên (α) ∩ (SBC) = NP
nên (α) ∩ (SBC) = NP
và NP // BC (1)
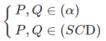 ⇒ (α) ∩ (SCD) = PQ
⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và 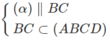 nên (α) ∩ (ABCD) = QM
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
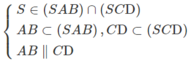 ⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒ 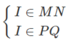
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.

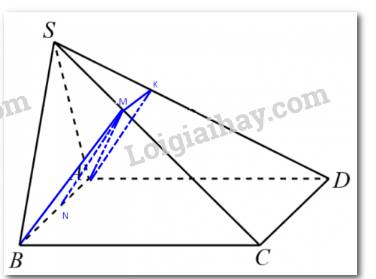
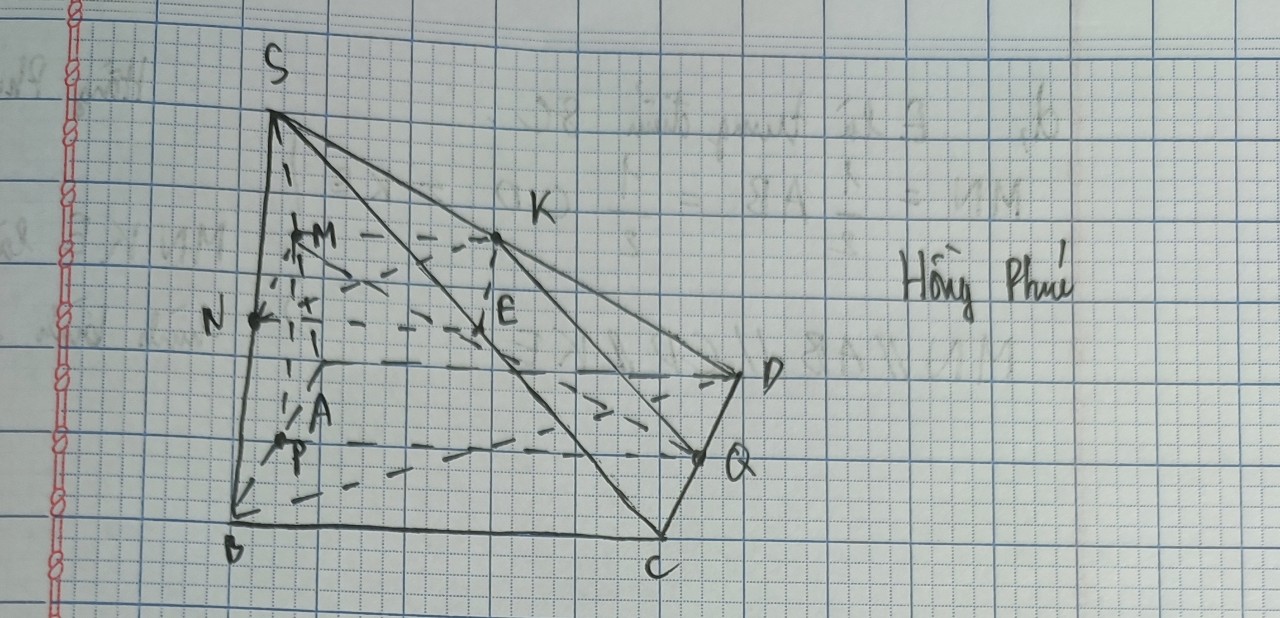
a) Ta có: \(\left( {ABM} \right) \cap \;\left( {ABCD} \right) = AB,\;\left( {ABCD} \right) \cap \;\left( {SCD} \right) = CD,\;AB//CD\).
Suy ra giao tuyến của (ABM) và (SCD) là đường thẳng qua M song song với AB và CD.
Qua M kẻ MK song song với CD (K thuộc SD).
Vậy, K là giao điểm của (AMN) và SD.
Xét tam giác SCD ta có: MK //CD suy ra \(\frac{{SK}}{{SD}} = \frac{{SM}}{{SC}} = \frac{1}{3}\)
b) Xét tam giác SCD ta có: MK //CD suy ra \(\frac{{MK}}{{CD}} = \frac{{SM}}{{SC}} = \frac{1}{3}\)
Lại có \(\frac{{AN}}{{AB}} = \frac{1}{3}\), AB=CD suy ra AN = MK.
Xét tứ giác ANMK ta có: AN = MK, AN // MK suy ra ANMK là hình bình hành.
Do đó MN // AK hay MN // (SAD).