Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình câu c là tui vẽ riêng ra cho dễ nhìn thôi, còn hình vẽ trình bày vô bài lấy hình chung ở câu a và b nhó :v



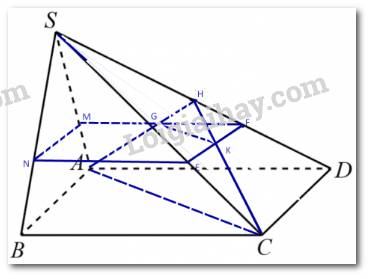
a) Xét tam giác HAC ta có: GH = 2GA, HK = 2KC suy ra GK // AC hay GK // (ABCD).
b) (MNEF) // (ABCD) do đó MN // AB, NE // BC, EF // CD, MF // AD
Lại có AB // CD, AD // BC suy ra MN // EF, MF // NE.
Suy ra, tứ giác MNEF là hình bình hành.

a) S là điểm chung của hai mặt phẳng (SAB) và (SCD) mà AB // CD
Từ S kẻ Sx sao cho Sx // AB // CD nên Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Gọi E là trung điểm của AB
G là trọng tâm tam giác SAB nên \(\frac{{EG}}{{SE}} = \frac{1}{3}\)
N là trọng tâm tam giác ABC nên\(\frac{{EN}}{{EC}} = \frac{1}{3}\)
Theo Ta lét, suy ra GN // SC mà SC \( \subset \) (SAC). Do đó, GN // (SAC)

Đáp án A
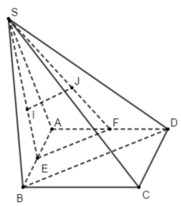
Tam giác SAB có I là trọng tâm và E là trung điểm của AB
Nên ta có S I S E = 2 3 (1)
Tam giác SAD có J là trọng tâm và F là trung điểm của AD
Nên ta có S J S F = 2 3 (2)
Từ (1) và (2) ta có: IJ // EF (3) (định lý Ta-lét trong tam giác SEF)
Tam giác ABD có EF là đường trung bình nên EF // BD (4)
Từ (3) và (4) suy ra IJ // BD
Mà BD (SBD)
Do đó IJ // (SBD).
Trong mp(SDA), gọi E là giao điểm của SG với AD
Trong mp(SBC), gọi K là giao điểm của SH với BC
Xét ΔSAD có
G là trọng tâm của ΔSAD
E là giao điểm của SG với AD
Do đó: E là trung điểm của AD
Xét ΔSBC có
H là trọng tâm của ΔSBC
SH cắt BC tại K
Do đó: K là trung điểm của BC
Xét hình thang ABCD(AB//CD) có
E,K lần lượt là trung điểm của AD,BC
=>EK là đường trung bình
=>EK//AB
Xét ΔSDE có
SE là đường trung tuyến
G là trọng tâm
Do đó: \(\dfrac{SG}{SE}=\dfrac{2}{3}\)
Xét ΔSBC có
H là trọng tâm của ΔSBC
SK là đường trung tuyến
Do đó: \(\dfrac{SH}{SK}=\dfrac{2}{3}\)
Xét ΔSEK có \(\dfrac{SG}{SE}=\dfrac{SH}{SK}\left(=\dfrac{2}{3}\right)\)
nên GH//EK
mà EK//AB
nên GH//AB
Ta có: GH//AB
AB\(\subset\)(SAB)
GH không nằm trong mp(SAB)
Do đó: GH//(SAB)