Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S A B C I H O K
a) \(SB^2=AS^2+AB^2=AS^2+AC^2=SC^2\Rightarrow SB=SC\) => \(\Delta\)SBC cân tại S
Do đó: AO,SH cắt nhau tại trung điểm I của cạnh BC
Xét \(\Delta\)SBC: trực tâm H, đường cao SI => \(IH.IS=IB.IC\)(1)
Tương tự: \(IB.IC=IO.IA\)(2)
Từ (1);(2) => \(IH.IS=IO.IA\)=> \(\Delta\)IHO ~ \(\Delta\)IAS => ^IHO = ^IAS = 900 => OH vuông góc IS (3)
Ta có: BC vuông góc với AI,AS => BC vuông góc với (SAI) => BC vuông góc OH (4)
Từ (3);(4) => OH vuông góc (SBC).
b) Xét tam giác SKI: IO vuông góc SK tại A, KO vuông góc SI tại H (cmt) => O là trực tâm tam giác SKI
Vậy SO vuông góc IK.

a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)

a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: BC vuông góc (SAM)
=>BC vuông góc SM
=>(SM;(ABC))=90 độ

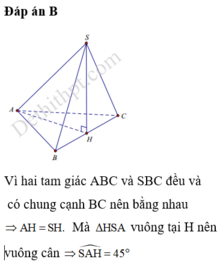
\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(SH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều SBC cạnh a)
\(AH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều ABC cạnh a)
\(tan\widehat{SAH}=\dfrac{SH}{AH}=1\Rightarrow\widehat{SAH}=45^0\)
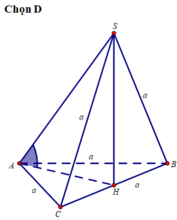

a.
Do ABC đều \(\Rightarrow\) AI là trung tuyến đồng thời là đường cao
\(\Rightarrow AI\perp BC\) (1)
SBC vuông cân tại S \(\Rightarrow SI\) là trung tuyến kiêm đường cao
\(\Rightarrow SI\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAI\right)\Rightarrow BC\perp SA\)
b.
\(SA>AI\Rightarrow\widehat{SIA}>\widehat{ASI}\Rightarrow\widehat{ASI}\) là góc nhọn
Do ABC đều \(\Rightarrow AI=\dfrac{a\sqrt{3}}{2}\)
SBC vuông cân tại S \(\Rightarrow SI=\dfrac{1}{2}BC=\dfrac{a}{2}\)
Áp dụng định lý hàm sin cho tam giác SAI:
\(\dfrac{SI}{sin\widehat{IAS}}=\dfrac{AI}{sin\widehat{ASI}}\Rightarrow sin\widehat{ASI}=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{ASI}=60^0\) (do \(\widehat{ASI}\) nhọn)
\(\Rightarrow=180^0-\left(30^0+60^0\right)=90^0\)
Hay \(SI\perp IA\)