Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
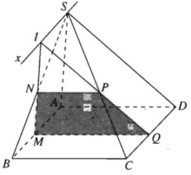
a) Vì M ∈ (SAB)
Và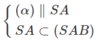 
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và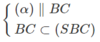 
nên (α) ∩ (SBC) = NP
và NP // BC (1)
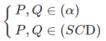⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và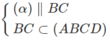 
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
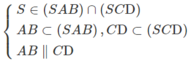⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒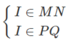 
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.
Gọi (α) là mặt phẳng qua O song song với AB và SC.
AB // (α) nên (α) cắt mp(ABCD) theo giao tuyến qua O và song song với AB. Gọi M, N lần lượt là giao điểm của đường thẳng qua O song song AB với BC và AD.
Trong mặt phẳng (SAC) kẻ OP // SC (P ϵ AS) (α) cắt mp(SAB) theo giao tuyến PQ // AB (Q ϵ SB)
Thiết diện cần tìm là tứ giác MNPQ.
Tứ giác MNPQ có PQ // MN nên MNPQ là hình thang.
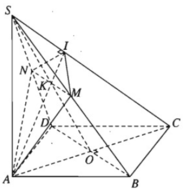
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
b) Ta có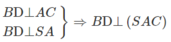 
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.
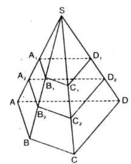
a) Chứng minh B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD
Ta có:
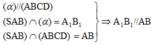
⇒ A 1 B 1 là đường trung bình của tam giác SAB.
⇒ B 1 là trung điểm của SB (đpcm)
*Chứng minh tương tự ta cũng được:
• C 1 là trung điểm của SC.
• D 1 là trung điểm của SD.
b) Chứng minh B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .
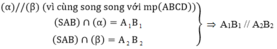
⇒ A 2 B 2 là đường trung bình của hình thang A 1 B 1 B A
⇒ B 2 là trung điểm của B 1 B
⇒ B 1 B 2 = B 2 B (đpcm)
*Chứng minh tương tự ta cũng được:
• C 2 là trung điểm của C 1 C 2 ⇒ C 1 C 2 = C 2 C
• D 2 là trung điểm của D 1 D 2 ⇒ D 1 D 2 = D 2 D .
c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A 1 B 1 C 1 D 1 . A B C D v à A 2 B 2 C 2 D 2 . A B C D
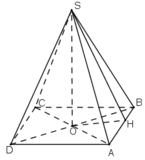
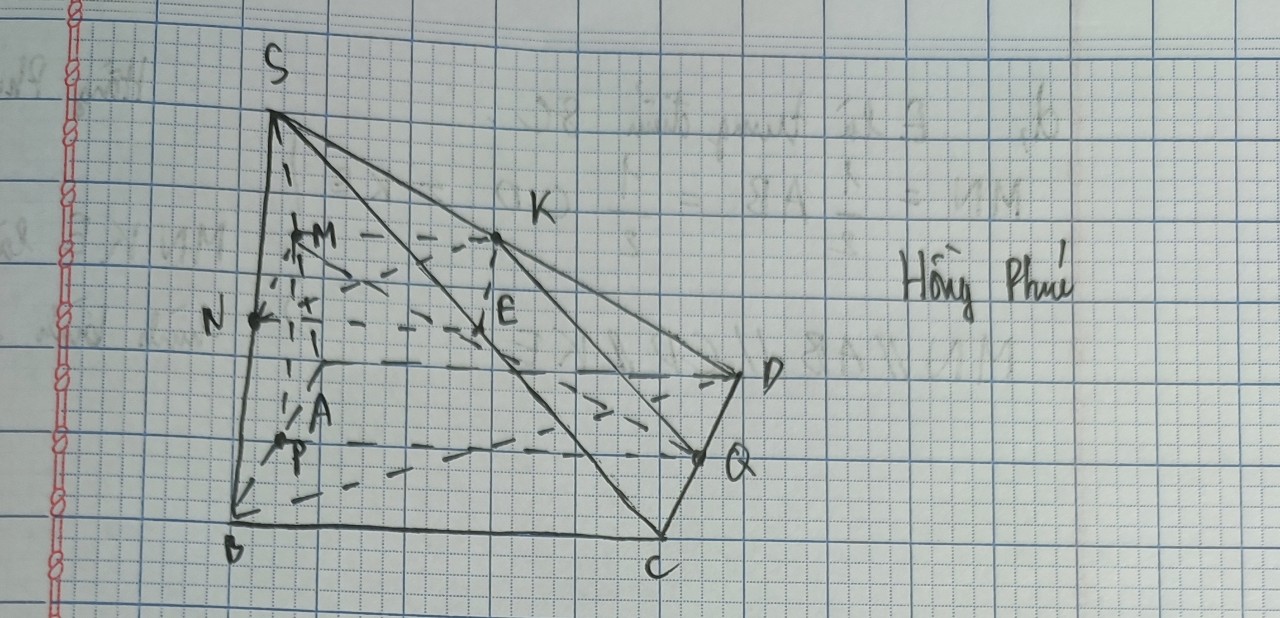
a)
+ Do ABCD là hình bình hành có tâm O- giao điểm hai đường chéo
=> O là trung điểm AC và BD( tính chất hình bình hành)
* Xét tam giác SAC có SA= SC nên tam giác SAC cân tại S
Lại có SO là đường trung tuyến nên đồng thời là đường cao: SO ⊥ AC
+ Tương tự, tam giác SBD cân tại S có SO là đường trung tuyến nên đồng thời là đường cao:
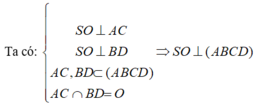
b) SO ⊥ (α) ⇒ SO ⊥ AB.
Lại có: SH ⊥ AB;
SO, SH ⊂ (SOH) và SO ∩ SH
⇒ AB ⊥ (SOH).
Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)
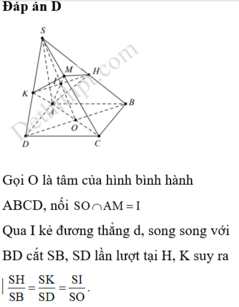
Trong tam giác A'BC, có IJ là đường trung bình
\(\Rightarrow IJ//BC\Rightarrow IJ//\left(ABC\right)\)
Qua O kẻ đường thẳng song song BC lần lượt cắt AB và AC tại E và F
\(\Rightarrow EF\in\left(IJO\right)\)
Trong mặt phẳng (ABB'A'), nối EI kéo dài cắt A'B' tại P
Trong mặt phẳng (ACC'A'), nối JF kéo dài cắt A'C' tại Q
\(\Rightarrow PQFE\) là tiết diện của (IJO) và lăng trụ
Mặt khác (ABC) và (A'B'C') là 2 mp song song nên \(PQ//EF\), do tính đối xứng của hai hình vuông ABB'A' và ACC'A' nên EP=FQ
\(\Rightarrow PQFE\) là hình thang cân
O là trọng tâm đáy \(\Rightarrow\frac{AE}{AB}=\frac{AF}{AC}=\frac{EF}{BC}=\frac{2}{3}\Rightarrow AE=AF=EF=\frac{2a}{3}\)
Talet \(\Rightarrow\frac{CF}{A'Q}=\frac{A'J}{JC}=1\Rightarrow A'Q=CF=\frac{a}{3}\)
Tương tự có \(A'P=\frac{a}{3}\Rightarrow PQ=\frac{a}{3}\)
Lấy K trên AB sao cho \(AK=\frac{a}{3}\Rightarrow PK||AA'\Rightarrow PK\perp AB\) và \(PK=AA'=a\)
\(EP=\sqrt{PK^2+EK^2}=\sqrt{a^2+\left(\frac{a}{3}\right)^2}=\frac{a\sqrt{10}}{3}\)
Hình thang cân có đủ 3 kích thước (2 cạnh đáy, cạnh bên), bạn tự tính diện tích ra nhé