Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

SA vuông góc (P)
SA vuông góc (ABC)
=>(P)//(ABC)
=>B'C'//BC

Tham khảo:
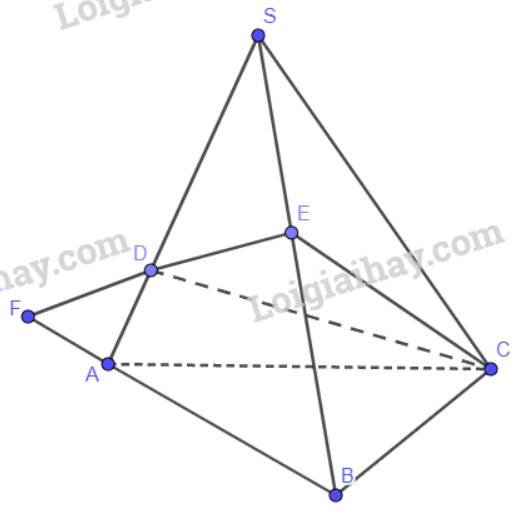
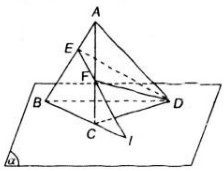
a) Ta có các điểm D, E đều nằm trong mp(SAB) nên đường thẳng DE nằm trong mp (SAB).
b) F thuộc AB suy ra F nằm trong mp (SAB).
F thuộc DE suy ra F nằm trong mp(CDE).
Do đó, F là điểm chung của hai mặt phẳng (SAB) và (CDE).

1:
a: \(D\in SA\subset\left(SAB\right);E\in SB\subset\left(SAB\right)\)
Do đó: \(DE\subset\left(SAB\right)\)
b: \(F\in AB\subset\left(SAB\right)\)
\(F\in DE\subset\left(CDE\right)\)
Do đó: \(F\in\left(SAB\right)\cap\left(CDE\right)\)
2:
\(N\in AB\subset\left(ABM\right);N\in CD\subset\left(SCD\right)\)
Do đó: \(N\in\left(ABM\right)\cap\left(SCD\right)\)
\(M\in SC\subset\left(SCD\right);M\in MB\subset\left(ABM\right)\)
Do đó: \(M\in\left(ABM\right)\cap\left(SCD\right)\)
Do đó: \(\left(ABM\right)\cap\left(SCD\right)=MN\)

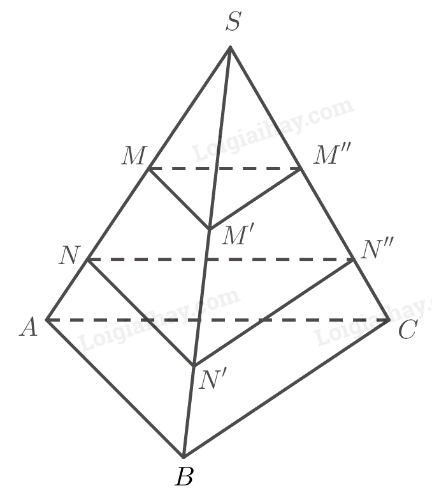
Ta có: \(\left( {MM'M''} \right)\parallel \left( {NN'N''} \right)\parallel \left( {ABC} \right)\) nên theo định lí Thalès ta có:
\(\frac{{SM}}{{SA}} = \frac{{SM'}}{{SB}} \Leftrightarrow SM' = \frac{{SM.SB}}{{SA}} = \frac{{4.12}}{9} = \frac{{16}}{3}\)
\(\frac{{SA}}{{SB}} = \frac{{MN}}{{M'N'}} \Leftrightarrow M'N' = \frac{{MN.SB}}{{SA}} = \frac{{3.12}}{9} = 4\)
\(\frac{{SA}}{{SC}} = \frac{{MN}}{{M''N''}} \Leftrightarrow M''N'' = \frac{{MN.SC}}{{SA}} = \frac{{3.15}}{9} = 5\)
\(\frac{{SA}}{{SC}} = \frac{{NA}}{{N''C}} \Leftrightarrow N''C = \frac{{NA.SC}}{{SA}} = \frac{{2.15}}{9} = \frac{{10}}{3}\)

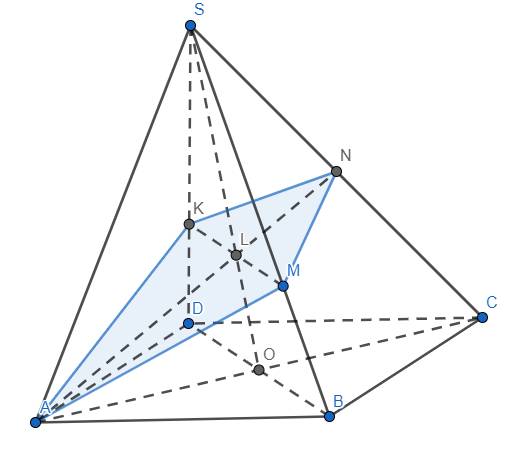
a) Gọi \(O=AC\cap BD\). Khi đó \(O\in\left(SAC\right)\cap\left(SBD\right)\). Lại có \(S\in\left(SAC\right)\cap\left(SBD\right)\) nên SO chính là giao tuyến của (SAC) và (SBD).
b) Trong mp (AMNK) cho \(AN\cap MK=L\). Do \(AN\subset\left(SAC\right),MK\subset\left(SBD\right)\) nên \(L\in\left(SAC\right)\cap\left(SBD\right)\) nên \(L\in SO\). \(\Rightarrow\) L là trọng tâm tam giác SAC \(\Rightarrow\dfrac{SL}{LO}=2\). Mà \(\dfrac{SM}{MB}=2\) nên \(\dfrac{SL}{LO}=\dfrac{SM}{MB}\Rightarrow\) LM//BO hay MK//BD, suy ra đpcm.

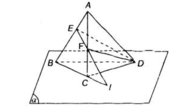
a) E ∈ AB mà AB ⊂ (ABC)
⇒ E ∈ (ABC)
F ∈ AC mà AC ⊂ (ABC)
⇒ F ∈ (ABC)
Đường thẳng EF có hai điểm E, F cùng thuộc mp(ABC) nên theo tính chất 3 thì EF ⊂ (ABC).
b) I ∈ BC mà BC ⊂ (BCD) nên I ∈ (BCD) (1)
I ∈ EF mà EF ⊂ (DEF) nên I ∈ (DEF) (2)
Từ (1) và (2) suy ra I là điểm chung của hai mặt phẳng (BCD) và (DEF).

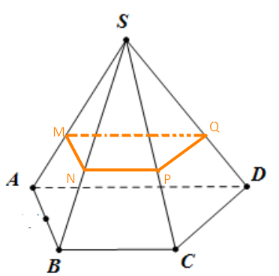
Xét tam giác SAD có: \(\dfrac{MA}{MS}=\dfrac{QD}{QS}\) suy ra MQ // AD do đó MQ // (ABCD)
Tương tự ta có: QP // (ABCD)
Vậy mp(MPQ) // mp(ABCD).
Lập luận tương tự, ta có mp(NPQ) // (ABCD).
Hai mặt phẳng (MPQ) và (NPQ) cùng đi qua điểm P và cùng song song với mặt phẳng (ABCD) nên hai mặt phẳng đó trùng nhau, tức bốn điểm M, N, P, Q đồng phẳng.

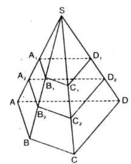
a) Chứng minh B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD
Ta có:
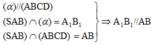
⇒ A 1 B 1 là đường trung bình của tam giác SAB.
⇒ B 1 là trung điểm của SB (đpcm)
*Chứng minh tương tự ta cũng được:
• C 1 là trung điểm của SC.
• D 1 là trung điểm của SD.
b) Chứng minh B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .
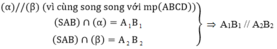
⇒ A 2 B 2 là đường trung bình của hình thang A 1 B 1 B A
⇒ B 2 là trung điểm của B 1 B
⇒ B 1 B 2 = B 2 B (đpcm)
*Chứng minh tương tự ta cũng được:
• C 2 là trung điểm của C 1 C 2 ⇒ C 1 C 2 = C 2 C
• D 2 là trung điểm của D 1 D 2 ⇒ D 1 D 2 = D 2 D .
c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A 1 B 1 C 1 D 1 . A B C D v à A 2 B 2 C 2 D 2 . A B C D